Sharing, Space Leaks, and Conduit and friends

Edsko de Vries – Thursday, 29 September 2016

all coding laziness  
TL;DR: Sharing conduit values leads to space leaks. Make sure that conduits are completely reconstructed on every call to runConduit; this implies we have to be careful not to create any (potentially large) conduit CAFs (skip to the final section “Avoiding space leaks” for some details on how to do this). Similar considerations apply to other streaming libraries and indeed any Haskell code that uses lazy data structures to drive computation.

Motivation

We use large lazy data structures in Haskell all the time to drive our programs. For example, consider

main1 :: IO ()
main1 = forM_ [1..5] $ \_ -> mapM_ print [1 .. 1000000]

It’s quite remarkable that this works and that this program runs in constant memory. But this stands on a delicate cusp. Consider the following minor variation on the above code:

ni_mapM_ :: (a -> IO b) -> [a] -> IO ()
{-# NOINLINE ni_mapM_ #-}
ni_mapM_ = mapM_

main2 :: IO ()
main2 = forM_ [1..5] $ \_ -> ni_mapM_ print [1 .. 1000000]

This program runs, but unlike main1, it has a maximum residency of 27 MB; in other words, this program suffers from a space leak. As it turns out, main1 was running in constant memory because the optimizer was able to eliminate the list altogether (due to the fold/build rewrite rule), but it is unable to do so in main2.

But why is main2 leaking? In fact, we can recover constant space behaviour by recompiling the code with -fno-full-laziness. The full laziness transformation is effectively turning main2 into

longList :: [Integer]
longList = [1 .. 1000000]

main3 :: IO ()
main3 = forM_ [1..5] $ \_ -> ni_mapM_ print longList

The first iteration of the forM_ loop constructs the list, which is then retained to be used by the next iterations. Hence, the large list is retained for the duration of the program, which is the beforementioned space leak.

The full laziness optimization is taking away our ability to control when data structures are not shared. That ability is crucial when we have actions driven by large lazy data structures. One particularly important example of such lazy structures that drive computation are conduits or pipes. For example, consider the following conduit code:

import qualified Data.Conduit as C

countConduit :: Int -> C.Sink Char IO ()
countConduit cnt = do
    mi <- C.await
    case mi of
      Nothing -> liftIO (print cnt)
      Just _  -> countConduit $! cnt + 1

getConduit :: Int -> C.Source IO Char
getConduit 0 = return ()
getConduit n = do
    ch <- liftIO getChar
    C.yield ch
    getConduit (n - 1)

Here countConduit is a sink that counts the characters it receives from upstream, and getConduit n is a conduit that reads n characters from the console and passes them downstream.

To illustrate what might go wrong, we will use the following exception handler throughout this blog post5:

retry :: IO a -> IO a
retry io = do
    ma <- try io
    case ma of
      Right a -> return a
      Left (_ :: SomeException) -> retry io

The important point to notice about this exception handler is that it retains a reference to the action io as it executes that action, since it might potentially have to execute it again if an exception is thrown. However, all the space leaks we discuss in this blog post arise even when an exception is never thrown and hence the action is run only once; simply maintaining a reference to the action until the end of the program is enough to cause the space leak.

If we use this exception handler as follows:

main :: IO ()
main = retry $ C.runConduit $ getConduit 1000000 C.=$= countConduit 0

we again end up with a large space leak, this time of type Pipe and ->Pipe (conduit’s internal type):

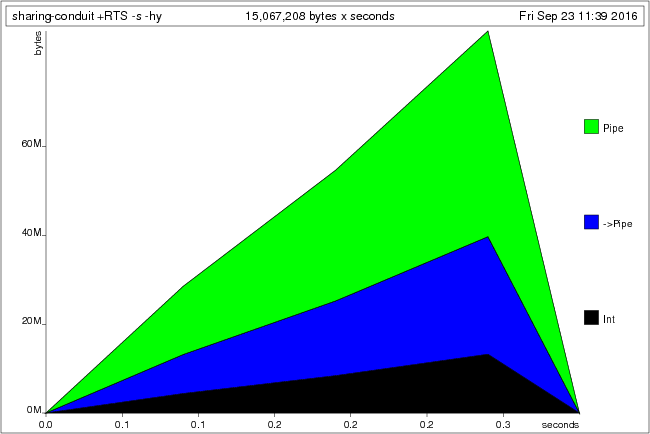
Although the values that stream through the conduit come from IO, the conduit itself is fully constructed and retained in memory. In this blog post we examine what exactly is being retained here, and why. We will finish with some suggestions on how to avoid such space-leaks, although sadly there is no easy answer. Note that these problems are not specific to the conduit library, but apply equally to all other similar libraries.

We will not assume any knowledge of conduit but start from first principles; however, if you have never used any of these libraries before this blog post is probably not the best starting point; you might for example first want to watch my presentation Lazy I/O and Alternatives in Haskell.

Lists

Before we look at the more complicated case, let’s first consider another program using just lists:

main :: IO ()
main = retry $ ni_mapM_ print [1..1000000]

This program suffers from a space leak for similar reasons to the example with lists we saw in the introduction, but it’s worth spelling out the details here: where exactly is the list being maintained?

Recall that the IO monad is effectively a state monad over a token RealWorld state (if that doesn’t make any sense to you, you might want to read ezyang’s article Unraveling the mystery of the IO monad first). Hence, ni_mapM_ (just a wrapper around mapM_) is really a function of three arguments: the action to execute for every element of the list, the list itself, and the world token. That means that

ni_mapM_ print [1..1000000]

is a partial application, and hence we are constructing a PAP object. Such a PAP object is an runtime representation of a partial application of a function; it records the function we want to execute (ni_mapM_), as well as the arguments we have already provided. It is this PAP object that we give to retry, and which retry retains until the action completes because it might need it in the exception handler. The long list in turn is being retained because there is a reference from the PAP object to the list (as one of the arguments that we provided).

Full laziness does not make a difference in this example; whether or not that [1 .. 10000000] expression gets floated out makes no difference.

Reminder: Conduits/Pipes

Just to make sure we don’t get lost in the details, let’s define a simple conduit-like or pipe-like data structure:

data Pipe i o m r =
    Yield o (Pipe i o m r)
  | Await (Either r i -> Pipe i o m r)
  | Effect (m (Pipe i o m r))
  | Done r

A pipe or a conduit is a free monad which provides three actions:

  1. Yield a value downstream
  2. Await a value from upstream
  3. Execute an effect in the underlying monad.

The argument to Await is passed an Either; we give it a Left value if upstream terminated, or a Right value if upstream yielded a value.1

This definition is not quite the same as the one used in real streaming libraries and ignores various difficulties (in particular exception safely, as well as other features such as leftovers); however, it will suffice for the sake of this blog post. We will use the terms “conduit” and “pipe” interchangeably in the remainder of this article.

Sources

The various Pipe constructors differ in their memory behaviour and the kinds of space leaks that they can create. We therefore consider them one by one. We will start with sources, because their memory behaviour is relatively straightforward.

A source is a pipe that only ever yields values downstream.2 For example, here is a source that yields the values [n, n-1 .. 1]:

yieldFrom :: Int -> Pipe i Int m ()
yieldFrom 0 = Done ()
yieldFrom n = Yield n $ yieldFrom (n - 1)

We could “run” such a pipe as follows:

printYields :: Show o => Pipe i o m () -> IO ()
printYields (Yield o k) = print o >> printYields k
printYields (Done ())   = return ()

If we then run the following program:

main :: IO ()
main = retry $ printYields (yieldFrom 1000000)

we get a space leak. This space leak is very similar to the space leak we discussed in section Lists above, with Done () playing the role of the empty list and Yield playing the role of (:). As in the list example, this program has a space leak independent of full laziness.

Sinks

A sink is a conduit that only ever awaits values from upstream; it never yields anything downstream.2 The memory behaviour of sinks is considerably more subtle than the memory behaviour of sources and we will examine it in detail. As a reminder, the constructor for Await is

data Pipe i o m r = Await (Either r i -> Pipe i o m r) | ...

As an example of a sink, consider this pipe that counts the number of characters it receives:

countChars :: Int -> Pipe Char o m Int
countChars cnt =
    Await $ \mi -> case mi of
      Left  _ -> Done cnt
      Right _ -> countChars $! cnt + 1

We could “run” such a sink by feeding it a bunch of characters; say, 1000000 of them:

feed :: Char -> Pipe Char o m Int -> IO ()
feed ch = feedFrom 10000000
  where
    feedFrom :: Int -> Pipe Char o m Int -> IO ()
    feedFrom _ (Done r)  = print r
    feedFrom 0 (Await k) = feedFrom 0     $ k (Left 0)
    feedFrom n (Await k) = feedFrom (n-1) $ k (Right ch)

If we run this as follows and compile with optimizations enabled, we once again end up with a space leak:

main :: IO ()
main = retry $ feed 'A' (countChars 0)

We can recover constant space behaviour by disabling full laziness; however, the effect of full laziness on this example is a lot more subtle than the example we described in the introduction.

Full laziness

Let’s take a brief moment to describe what full laziness is, exactly. Full laziness is one of the optimizations that ghc applies by default when optimizations are enabled; it is described in the paper “Let-floating: moving bindings to give faster programs”. The idea is simple; if we have something like

f = \x y -> let e = .. -- expensive computation involving x but not y
            in ..

full laziness floats the let binding out over the lambda to get

f = \x = let e = .. in \y -> ..

This potentially avoids unnecessarily recomputing e for different values of y. Full laziness is a useful transformation; for example, it turns something like

f x y = ..
  where
    go = .. -- some local function

into

f x y   = ..
f_go .. = ..

which avoids allocating a function closure every time f is called. It is also quite a notorious optimization, because it can create unexpected CAFs (constant applicative forms; top-level definitions of values); for example, if you write

nthPrime :: Int -> Int
nthPrime n = allPrimes !! n
  where
    allPrimes :: [Int]
    allPrimes = ..

you might expect nthPrime to recompute allPrimes every time it is invoked; but full laziness might move that allPrimes definition to the top-level, resulting in a large space leak (the full list of primes would be retained for the lifetime of the program). This goes back to the point we made in the introduction: full laziness is taking away our ability to control when values are not shared.

Full laziness versus sinks

Back to the sink example. What exactly is full laziness doing here? Is it constructing a CAF we weren’t expecting? Actually, no; it’s more subtle than that. Our definition of countChars was

countChars :: Int -> Pipe Char o m Int
countChars cnt =
    Await $ \mi -> case mi of
      Left  _ -> Done cnt
      Right _ -> countChars $! cnt + 1

Full laziness is turning this into something more akin to

countChars' :: Int -> Pipe Char o m Int
countChars' cnt =
    let k = countChars' $! cnt + 1
    in Await $ \mi -> case mi of
                        Left  _ -> Done cnt
                        Right _ -> k

Note how the computation of countChars' $! cnt + 1 has been floated over the lambda; ghc can do that, since this expression does not depend on mi. So in memory the countChars 0 expression from our main function (retained, if you recall, because of the surrounding retry wrapper), develops something like this. It starts of as a simple thunk:

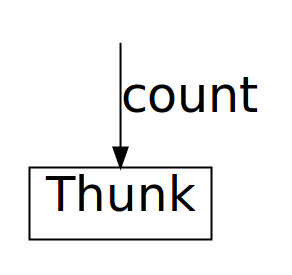
Then when feed matches on it, it gets reduced to weak head normal form, exposing the top-most Await constructor:

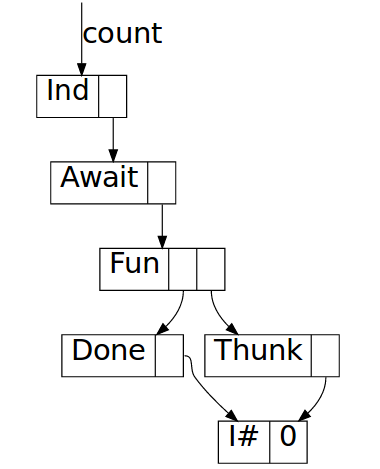
The body of the await is a function closure pointing to the function inside countChars (\mi -> case mi ..), which has countChars $! (cnt + 1) as an unevaluated thunk in its environment. Evaluating it one step further yields

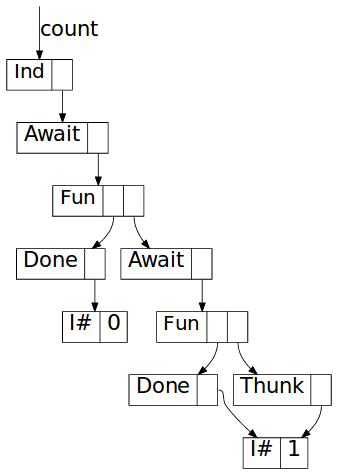
So where for a source the data structure in memory was a straightforward “list” consisting of Yield nodes, for a sink the situation is more subtle: we build up a chain of Await constructors, each of which points to a function closure which in its environment has a reference to the next Await constructor. This wouldn’t matter of course if the garbage collector could clean up after us; but if the conduit itself is shared, then this results in a space leak.

Without full laziness, incidentally, evaluating countChars 0 yields

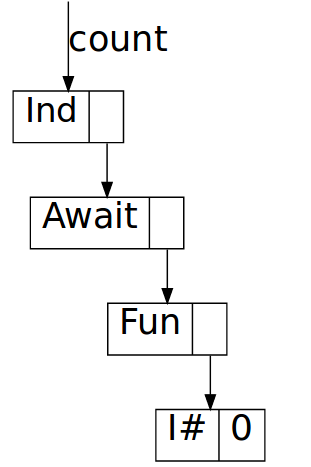
and the chain stops there; the only thing in the function closure now is cnt. Since we don’t allocate the next Yield constructor before running the function, we never construct a chain of Yield constructors and hence we have no space leak.

Depending on values

It is tempting to think that if the conduit varies its behaviour depending on the values it receives from upstream the same chain of Await constructors cannot be constructed and we avoid a space leak. For example, consider this variation on countChars which only counts spaces:

countSpaces :: Int -> Pipe Char o m Int
countSpaces cnt =
    Await $ \mi ->
      case mi of
        Left  _   -> Done cnt
        Right ' ' -> countSpaces $! cnt + 1
        Right _   -> countSpaces $! cnt

If we substitute this conduit for countChars in the previous program, do we fare any better? Alas, the memory behaviour of this conduit, when shared, is in fact far, far worse.

The reason is that both the countSpaces $! cnt + 1 and the expression countSpaces $! cnt can both be floated out by the full laziness optimization. Hence, now every Await constructor will have a function closure in its payload with two thunks, one for each alternative way to execute the conduit. What’s more, both of these thunks will are retained as long as we retain a reference to the top-level conduit.

We can neatly illustrate this using the following program:

main :: IO ()
main = do
    let count = countSpaces 0
    feed ' ' count
    feed ' ' count
    feed ' ' count
    feed 'A' count
    feed 'A' count
    feed 'A' count

The first feed ' ' explores a path through the conduit where every character is a space; so this constructs (and retains) one long chain of Await constructors. The next two calls to feed ' ' however walk over the exact same path, and hence memory usage does not increase for a while. But then we explore a different path, in which every character is a non-space, and hence memory behaviour will go up again. Then during the second call to feed 'A' memory usage is stable again, until we start executing the last feed 'A', at which point the garbage collector can finally start cleaning things up:

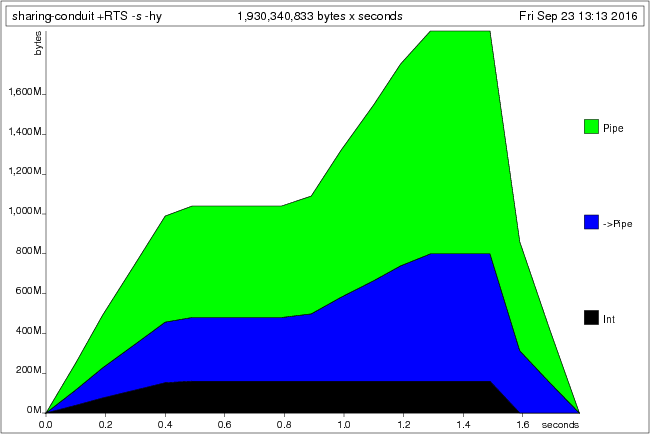
What’s worse, there is an infinite number of paths through this conduit. Every different combination of space and non-space characters will explore a different path, leading to combinatorial explosion and terrifying memory usage.

Effects

The precise situation for effects depends on the underlying monad, but let’s explore one common case: IO. As we will see, for the case of IO the memory behaviour of Effect is actually similar to the memory behaviour of Await. Recall that the Effect constructor is defined as

data Pipe i o m r = Effect (m (Pipe i o m r)) | ...

Consider this simple pipe that prints the numbers [n, n-1 .. 1]:

printFrom :: Int -> Pipe i o IO ()
printFrom 0 = Done ()
printFrom n = Effect $ print n >> return (printFrom (n - 1))

We might run such a pipe using3:

runPipe :: Show r => Pipe i o IO r -> IO ()
runPipe (Done r)   = print r
runPipe (Effect k) = runPipe =<< k

In order to understand the memory behaviour of Effect, we need to understand how the underlying monad behaves. For the case of IO, IO actions are state transformers over a token RealWorld state. This means that the Effect constructor actually looks rather similar to the Await constructor. Both have a function as payload; Await a function that receives an upstream value, and Effect a function that receives a RealWorld token. To illustrate what printFrom might look like with full laziness, we can rewrite it as

printFrom :: Int -> Pipe i o IO ()
printFrom n =
    let k = printFrom (n - 1)
    in case n of
         0 -> Done ()
         _ -> Effect $ IO $ \st -> unIO (print n >> return k) st

If we visualize the heap (using ghc-vis), we can see that it does indeed look very similar to the picture for Await:

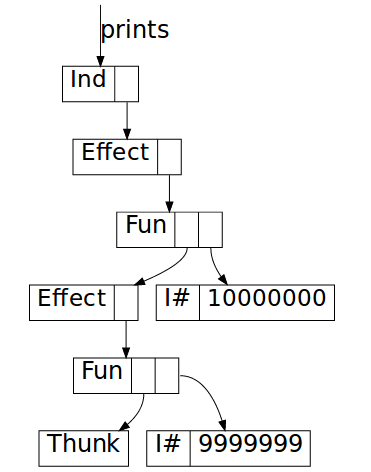
Increasing sharing

If we cannot guarantee that our conduits are not shared, then perhaps we should try to increase sharing instead. If we can avoid allocating these chains of pipes, but instead have pipes refer back to themselves, perhaps we can avoid these space leaks.

In theory, this is possible. For example, when using the conduit library, we could try to take advantage of monad transformers and rewrite our feed source and our count sink as:

feed :: Source IO Char
feed = evalStateC 1000000 go
  where
    go :: Source (StateT Int IO) Char
    go = do
      st <- get
      if st == 0
        then return ()
        else do put $! (st - 1) ; yield 'A' ; go

count :: Sink Char IO Int
count = evalStateC 0 go
  where
    go :: Sink Char (StateT Int IO) Int
    go = do
        mi <- await
        case mi of
          Nothing -> get
          Just _  -> modify' (+1) >> go

In both definitions go refers back to itself directly, with no arguments; hence, it ought to be self-referential, without any long chain of sources or sinks ever being constructed. This works; the following program runs in constant space:

main :: IO ()
main = retry $ print =<< (feed $$ count)

However, this kind of code is extremely brittle. For example, consider the following minor variation on count:

count :: Sink Char IO Int
count = evalStateC 0 go
  where
    go :: Sink Char (StateT Int IO) Int
    go = withValue $ \_ -> modify' (+1) >> go

    withValue :: (i -> Sink i (StateT Int IO) Int)
              -> Sink i (StateT Int IO) Int
    withValue k = do
      mch <- await
      case mch of
        Nothing -> get
        Just ch -> k ch

This seems like a straight-forward variation, but this code in fact suffers from a space leak again4. The optimized core version of this variation of count looks something like this:

count :: ConduitM Char Void (StateT Int IO) Int
count = ConduitM $ \k ->
    let countRec = modify' (+ 1) >> count
    in unConduitM await $ \mch ->
         case mch of
           Nothing -> unConduitM get      k
           Just _  -> unConduitM countRec k

In the conduit library, ConduitM is a codensity transformation of an internal Pipe datatype; the latter corresponds more or less to the Pipe datastructure we’ve been describing here. But we can ignore these details: the important point here is that this has the same typical shape that we’ve been studying above, with an allocation inside a lambda but before an await.

We can fix it by writing our code as

count :: Sink Char IO Int
count = evalStateC 0 go
  where
    go :: Sink Char (StateT Int IO) Int
    go = withValue goWithValue

    goWithValue :: Char -> Sink Char (StateT Int IO) Int
    goWithValue _ = modify' (+1) >> go

    withValue :: (i -> Sink i (StateT Int IO) Int)
              -> Sink i (StateT Int IO) Int
    withValue k = do
      mch <- await
      case mch of
        Nothing -> get
        Just ch -> k ch

Ironically, it would seem that full laziness here could have helped us by floating out that modify' (+1) >> go expression for us. The reason that it didn’t is probably related to the exact way the k continuation is threaded through in the compiled code (I simplified a bit above). Whatever the reason, tracking down problems like these is difficult and incredibly time consuming; I’ve spent many many hours studying the output of -ddump-simpl and comparing before and after pictures. Not a particularly productive way to spend my time, and this kind of low-level thinking is not what I want to do when writing application level Haskell code!

Composed pipes

Normally we construct pipes by composing components together. Composition of pipes can be defined as

(=$=) :: Monad m => Pipe a b m r -> Pipe b c m r -> Pipe a c m r
{-# NOINLINE (=$=) #-}
_         =$= Done   r   = Done r
u         =$= Effect   d = Effect $ (u =$=) <$> d
u         =$= Yield  o d = Yield o (u =$= d)
Yield o u =$= Await    d = u =$= d (Right o)
Await   u =$= Await    d = Await $ \ma -> u ma =$= Await d
Effect  u =$= Await    d = Effect $ (=$= Await d) <$> u
Done  r   =$= Await    d = Done r =$= d (Left r)

The downstream pipe “is in charge”; the upstream pipe only plays a role when downstream awaits. This mirrors Haskell’s lazy “demand-driven” evaluation model.

Typically we only run self-contained pipes that don’t have any Awaits or Yields left (after composition), so we are only left with Effects. The good news is that if the pipe components don’t consist of long chains, then their composition won’t either; at every Effect point we wait for either upstream or downstream to complete its effect; only once that is done do we receive the next part of the pipeline and hence no chains can be constructed.

On the other hand, of course composition doesn’t get rid of these space leaks either. As an example, we can define a pipe equivalent to the getConduit from the introduction

getN :: Int -> Pipe i Char IO Int
getN 0 = Done 0
getN n = Effect $ do
           ch <- getChar
           return $ Yield ch (getN (n - 1))

and then compose getN and countChars to get a runnable program:

main :: IO ()
main = retry $ runPipe $ getN 1000000 =$= countChars 0

This program suffers from the same space leaks as before because the individual pipelines component are kept in memory. As in the sink example, memory behaviour would be much worse still if there was different paths through the conduit network.

Summary

At Well-Typed we’ve been developing an application for a client to do streaming data processing. We’ve been using the conduit library to do this, with great success. However, occassionally space leaks arise that difficult to fix, and even harder to track down; of course, we’re not the first to suffer from these problems; for example, see ghc ticket #9520 or issue #6 for the streaming library (a library similar to conduit).

In this blog post we described how such space leaks arise. Similar space leaks can arise with any kind of code that uses large lazy data structures to drive computation, including other streaming libraries such as pipes or streaming, but the problem is not restricted to streaming libraries.

The conduit library tries to avoid these intermediate data structures by means of fusion rules; naturally, when this is successful the problem is avoided. We can increase the likelihood of this happening by using combinators such as folds etc., but in general the intermediate pipe data structures are difficult to avoid.

The core of the problem is that in the presence of the full laziness optimization we have no control over when values are not shared. While it is possible in theory to write code in such a way that the lazy data structures are self-referential and hence keeping them in memory does not cause a space leak, in practice the resulting code is too brittle and writing code like this is just too difficult. Just to provide one more example, in our application we had some code that looked like this:

go x@(C y _) = case y of
         Constr1 -> doSomethingWith x >> go
         Constr2 -> doSomethingWith x >> go
         Constr3 -> doSomethingWith x >> go
         Constr4 -> doSomethingWith x >> go
         Constr5 -> doSomethingWith x >> go

This worked and ran in constant space. But after adding a single additional clause to this pattern match, suddenly we reintroduced a space leak again:

go x@(C y _) = case y of
         Constr1 -> doSomethingWith x >> go
         Constr2 -> doSomethingWith x >> go
         Constr3 -> doSomethingWith x >> go
         Constr4 -> doSomethingWith x >> go
         Constr5 -> doSomethingWith x >> go
         Constr6 -> doSomethingWith x >> go

This was true even when that additional clause was never used; it had nothing to do with the change in the runtime behaviour of the code. Instead, when we added the additional clause some limit got exceeded in ghc’s bowels and suddenly something got allocated that wasn’t getting allocated before.

Full laziness can be disabled using -fno-full-laziness, but sadly this throws out the baby with the bathwater. In many cases, full laziness is a useful optimization. In particular, there is probably never any point allocation a thunk for something that is entirely static. We saw one such example above; it’s unexpected that when we write

go = withValue $ \_ -> modify' (+1) >> go

we get memory allocations corresponding to the modify' (+1) >> go expression.

Avoiding space leaks

So how do we avoid these space leaks? The key idea is pretty simple: we have to make sure the conduit is fully reconstructed on every call to runConduit. Conduit code typically looks like

runMyConduit :: Some -> Args -> IO r
runMyConduit some args =
    runConduit $ stage1 some
             =$= stage2 args
             ...
             =$= stageN

You should put all top-level calls to runConduit into a module of their own, and disable full laziness in that module by declaring

{-# OPTIONS_GHC -fno-full-laziness #-}

at the top of the file. This means the computation of the conduit (stage1 =$= stage2 .. =$= stageN) won’t get floated to the top and the conduit will be recomputed on every invocation of runMyConduit (note that this relies on runMyConduit to have some arguments; if it doesn’t, you should add a dummy one).

This might not be enough, however. In the example above, stageN is still a CAF, and the evalation of the conduit stage1 =$= ... =$= stageN will cause that CAF to be evaluated and potentially retained in memory. CAFs are fine for conduits that are guaranteed to be small, or that loop back onto themselves; however, as discussed in section “Increasing sharing”, writing such conduit values is not an easy task, although it is manageable for simple conduits.

To avoid CAFs, conduis like stageN must be given a dummy argument and full laziness must be disabled for the module where stageN is defined. But it’s more subtle than that; even if a conduit does have real (non-dummy) arguments, part of that conduit might still be independent of those arguments and hence be floated to the top by the full laziness optimization, creating yet more unwanted CAF values. Full laziness must again be disabled to stop this from happening.

If you are sure that full laziness cannot float anything harmful to the top, you can leave it enabled; however, verifying that this is the case is highly non-trivial. You can of course test the code, but if you are unlucky the memory leak will only arise under certain specific usage conditions. Moreover, a small modification to the codebase, the libraries it uses, or even the compiler, perhaps years down the line, might change the program and reintroduce a memory leak.

Proceed with caution.

Further reading

Addendum 1: ghc’s “state hack”

Let’s go back to the section about sinks; if you recall, we considered this example:

countChars :: Int -> Pipe Char o m Int
countChars cnt =
    let k = countChars $! cnt + 1
    in Await $ \mi -> case mi of
                        Left  _ -> Done cnt
                        Right _ -> k

feedFrom :: Int -> Pipe Char o m Int -> IO ()
feedFrom n (Done r)  = print r
feedFrom 0 (Await k) = feedFrom 0 $ k (Left 0)
feedFrom n (Await k) = feedFrom (n - 1) $ k (Right 'A')

main :: IO ()
main = retry $ feedFrom 10000000 (countChars 0)

We explained how countChars 0 results in a chain of Await constructors and function closures. However, you might be wondering, why would this be retained at all? After all, feedFrom is just an ordinary function, albeit one that computes an IO action. Why shouldn’t the whole expression

feedFrom 10000000 (countChars 0)

just be reduced to a single print 10000000 action, leaving no trace of the pipe at all? Indeed, this is precisely what happens when we disable ghc’s “state hack”; if we compile this program with -fno-state-hack it runs in constant space.

So what is the state hack? You can think of it as the opposite of the full laziness transformation; where full laziness transforms

     \x -> \y -> let e = <expensive> in ..    
~~>  \x -> let e = <expensive> in \y -> ..

the state hack does the opposite

     \x -> let e = <expensive> in \y -> ..
~~>  \x -> \y -> let e = <expensive> in ..

though only for arguments y of type State# <token>. In general this is not sound, of course, as it might duplicate work; hence, the name “state hack”. Joachim Breitner’s StackOverflow answer explains why this optimization is necessary; my own blog post Understanding the RealWorld provides more background.

Let’s leave aside the question of why this optimization exists, and consider the effect on the code above. If you ask ghc to dump the optimized core (-ddump-stg), and translate the result back to readable Haskell, you will realize that it boils down to a single line change. With the state hack disabled the last line of feedFrom is effectively:

feedFrom n (Await k) = IO $
    unIO (feedFrom (n - 1) (k (Right 'A')))

where IO and unIO just wrap and unwrap the IO monad. But when the state hack is enabled (the default), this turns into

feedFrom n (Await k) = IO $ \w ->
    unIO (feedFrom (n - 1) (k (Right 'A'))) w

Note how this floats the recursive call to feedFrom into the lambda. This means that

feedFrom 10000000 (countChars 0)

no longer reduces to a single print statement (after an expensive computation); instead, it reduces immediately to a function closure, waiting for its world argument. It’s this function closure that retains the Await/function chain and hence causes the space leak.

Addendum 2: Interaction with cost-centres (SCC)

A final cautionary tale. Suppose we are studying a space leak, and so we are compiling our code with profiling enabled. At some point we add some cost centres, or use -fprof-auto perhaps, and suddenly find that the space leak disappeared! What gives?

Consider one last time the sink example. We can make the space leak disappear by adding a single cost centre:

feed :: Char -> Pipe Char o m Int -> IO ()
feed ch = feedFrom 10000000
  where
    feedFrom :: Int -> Pipe Char o m Int -> IO ()
    feedFrom n p = {-# SCC "feedFrom" #-}
      case (n, p) of
        (_, Done r)  -> print r
        (0, Await k) -> feedFrom 0     $ k (Left 0)
        (_, Await k) -> feedFrom (n-1) $ k (Right ch)

Adding this cost centre effectively has the same result as specifying -fno-state-hack; with the cost centre present, the state hack can no longer float the computations into the lambda.

Footnotes

  1. The ability to detect upstream termination is one of the characteristics that sets conduit apart from the pipes package, in which this is impossible (or at least hard to do). Personally, I consider this an essential feature. Note that the definition of Pipe in conduit takes an additional type argument to avoid insisting that the type of the upstream return value matches the type of the downstream return value. For simplicity I’ve omitted this additional type argument here.

  2. Sinks and sources can also execute effects, of course; since we are interested in the memory behaviour of the indvidual constructors, we treat effects separately.

  3. runPipe is (close to) the actual runPipe we would normally use; we connect pipes that await or yield into a single self contained pipe that does neither.

  4. For these simple examples actually the optimizer can work its magic and the space leak doesn’t appear, unless evalStateC is declared NOINLINE. Again, for larger examples problems arise whether it’s inlined or not.

  5. The original definition of retry used in this blogpost was

    retry io = catch io (\(_ :: SomeException) -> retry io)

    but as Eric Mertens rightly points out, this is not correct as catch runs the exception handler with exceptions masked. For the purposes of this blog post however the difference is not important; in fact, none of the examples in this blog post run the exception handler at all.