Avoiding quadratic core code size with large records

Edsko will be talking about the problems discussed in this blog post in his Haskell Implementors’ Workshop talk this Sunday, Aug 22. The talk will be broadcast live on YouTube.

Consider a module that contains nothing but the definition of a single large record and some type class instances:

{-# OPTIONS_GHC -fplugin=RecordDotPreprocessor #-}

module Example where

import Data.Aeson
import Generics.SOP.JSON
import Generics.SOP.TH
import GHC.TypeLits

newtype T (i :: Nat) = MkT Word
  deriving (Show, Eq, ToJSON)

data R = MkR {
      f00 :: T 00
    , f01 :: T 01
      -- .. lots more ..
    , f98 :: T 98
    , f99 :: T 99
    }
  deriving (Eq, Show)

deriveGeneric ''R

instance ToJSON R where
  toJSON = gtoJSON defaultJsonOptions

As it stands—using ghc’s standard representation for records, along with the code generated by the RecordDotPreprocessor plugin and the Generic instance generated by generics-sop—this results in a core representation of a whopping 450,000 terms/types/coercions, takes 3 seconds to compile, and requires 500M of RAM to compile.¹

If we change this module to

module Example where

import Data.Aeson (ToJSON(..))
import Data.Record.Generic.JSON
import Data.Record.TH

import Test.Record.Size.Infra

largeRecord defaultLazyOptions [d|
    data R = MkR {
          f00 :: T 00
        , f01 :: T 01
          -- .. lots more ..
        , f98 :: T 98
        , f99 :: T 99
        }
      deriving (Eq, Show)
  |]

instance ToJSON R where
  toJSON = gtoJSON

we get a module with essentially the same functionality, but with a core size of a mere 14,000 terms/types/coercions, which compiles within 1 second and requires roughly 100M of RAM.

In this blog post we describe why this simple module generates so much code, and how the large-records library manages to reduce this by more than an order of magnitude.

We wrote this library because Juspay recently engaged Well-Typed’s services, and one of their requests to us was to try and improve compilation time and compilation memory requirements for their code base. Juspay very generously allowed us to make large-records open source, and it is now available on Hackage.

Quadratic code size at every level

The reason the core representation of our example module is so large is that unfortunately there are many examples of ghc and other libraries being accidentally quadratic. Before we look at some concrete examples, let’s first investigate where this quadratic code size is coming from. As we will see, it arises at every level: terms, types, type classes, and type level programming.

Warmup: terms

For our running example, we will want to have a record with lots of fields. To avoid some “accidental optimizations”, we’ll give each of those fields a different type. To make that a little bit easier, we’ll just introduce a single type that is indexed by a natural number, so that this one type definition gives us as many different types as we need:

data T (n :: Nat) = MkT Int

That out of the way, consider a record with lots of fields, such as

data R = MkR {
    f00 :: T 00
  , f01 :: T 01
  , f02 :: T 02
  -- .. lots more ..
  , f98 :: T 98
  , f99 :: T 99
  }

When we define a record, ghc will generate field accessors for all fields in the record. In other words, it will derive functions such as

f00 :: R -> T 0

These functions are not difficult to generate, of course. Each function is just a simple case statement:

f00 = \(r :: R) ->
    case r of
      MkR x00 x01 x02 x03 x04 x05 x06 x07 x08 x09
          x10 x11 x12 x13 x14 x15 x16 x17 x18 x19
          -- .. lots more ..
          x90 x91 x92 x93 x94 x95 x96 x97 x98 x99 ->
        x00

Although simple, this case statement mentions a lot of unused variables (99 of them, in fact). Moreover, each of those variables is annotated with their type. This means that this one function is actually rather large; ghc reports that it contains 5 terms and 202 types. The size of this function is clearly linear in the number n of fields we have; moreover, ghc will generate one function for each of those n fields; that means that simply declaring the record will already generate code that is O(n²) in size.

More subtle: types

Suppose we define an applicative “zip” function for R, something like

zipMyRecordWith ::
     Applicative f
  => (forall n. T n -> T n -> f (T n))
  -> R -> R -> f R
zipMyRecordWith f r r' =
        pure MkR
    <*> f (f00 r) (f00 r')
    <*> f (f01 r) (f01 r')
    <*> f (f02 r) (f02 r')
    -- .. lots more ..
    <*> f (f98 r) (f98 r')
    <*> f (f99 r) (f99 r')

Clearly the size of this function is at least linear in the number of record fields, that much is expected. However, -ddump-simpl tells us that this function contains 50,818 types! Where are all of those coming from?

Recall the type of (<*>):

(<*>) :: Applicative f => f (a -> b) -> f a -> f b

Those type variables need to be instantiated; f is always instantiated to the f type parameter passed to zipMyRecordWith, a is the type of the next field we’re applying, but what about b? Let’s annotate zipMyRecordWith with the types of a and b in pseudo-Haskell:

zipMyRecordWith ::
     Applicative f
  => (forall n. T n -> T n -> f (T n))
  -> R -> R -> f R
zipMyRecordWith f r r' =
        pure MkR
    <*> @(T 00) @(T 01 -> T 02 -> T 03 -> .. -> T 99 -> R) f (f00 r) (f00 r')
    <*> @(T 01) @(        T 02 -> T 03 -> .. -> T 99 -> R) f (f01 r) (f01 r')
    <*> @(T 02) @(                T 03 -> .. -> T 99 -> R) f (f02 r) (f02 r')
    -- .. lots more ..
    <*> @(T 98) @(                              T 99 -> R) f (f98 r) (f98 r')
    <*> @(T 99) @(                                      R) f (f99 r) (f99 r')

The first instantiation of (<*>) mentions the type of every single field; the second mentions the types of all-but-one field, the next of all-but-two, etc. This means that the size of this single function is once again O(n²) in the number of record fields.

Type class dictionaries

Suppose we wanted to capture the concept “some constraints c applied to the types of all fields in our record”:

class (
    c (T 00)
  , c (T 01)
  , c (T 02)
  -- .. lots more ..
  , c (T 98)
  , c (T 99)
  ) => Constraints_R c

This should be fine right? Right? Wrong.

When we declare a type class, we’re effectively constructing a record type with fields for each of the methods of the class; this record is known as the “dictionary” for the class. Superclass constraints translate to “subdictionaries”: when a class such as Ord has a superclass constraint on Eq, then the dictionary for Ord will have a field for an Eq dictionary.

This means that this definition of Constraints_R is actually of a very similar nature to the definition of R itself: it defines a record with 100 fields. And just like for the record, ghc will generate “field accessors” to extract the fields of this dictionary; put another way, those field accessors “prove” that if we know Constraints_R c, we also know c (T 00), c (T 01), etc. What do those field accessors look like? You guessed it, a big pattern match; in pseudo-Haskell:

$p1Constraints_R :: Constraints_R c => c (T 0)
$p1Constraints_R = \dict ->
    case dict of
      Constraints_R d00 d01 d02 d03 d04 d05 d06 d07 d08 d09
                    d10 d11 d12 d13 d14 d15 d16 d17 d18 d19
                    -- .. lots more ..
                    d90 d91 d92 d93 d94 d95 d96 d97 d98 d99 ->
        d00

Since ghc generates a projection like this for each superclass constraint, this once again results in code of size that is O(n²) in the number of record fields.

Type level induction

So far all our examples have been simple Haskell; for our next example, we’ll get a bit more advanced. Just like we can have list values, we can also have list types; for example, here is a type-level list of the indices of the T types used inside our running example record R:

type IndicesR = '[
    00, 01, 02, 03, 04, 05, 06, 07, 08, 09
  , 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
  -- .. lots more ..
  , 90, 91, 92, 93, 94, 95, 96, 97, 98, 99
  ]

There are many use cases for type level lists. For example, we can define a type NP such that NP f [x, y, .., z] is basically the same as (f x, f y, .., f z):

data NP (f :: k -> Type) (xs :: [k]) where
  Nil  :: NP f '[]
  (:*) :: f x -> NP f xs -> NP f (x ': xs)

If we have a T for every index in IndicesR, we can construct a value of our record:

npToR :: NP T IndicesR -> R
npToR (  f00 :* f01 :* f02 :* f03 :* f04 :* f05 :* f06 :* f07 :* f08 :* f09
      :* f10 :* f11 :* f12 :* f13 :* f14 :* f15 :* f16 :* f17 :* f18 :* f19
       -- .. lots more ..
      :* f90 :* f91 :* f92 :* f93 :* f94 :* f95 :* f96 :* f97 :* f98 :* f99
      :* Nil ) = MkR {..}

The compiled size of npToR is large, but it is linear in size (total size of 4441 terms, types and coercions for 100 fields, and a total size of 2241 for 50 fields). So far so good.

In order to get to the problem I’d like to illustrate in this section, we need one more concept. Suppose wanted to write a function that can construct a value of NP T xs for any xs:

mkNP :: NP T xs

This should be possible, since T is just a wrapper around an Int, and so all we need to do is generate as many Ts as there are elements in the type level list xs. However, xs is a type level list, and we cannot pattern match on types in Haskell; indeed, they do not even exist at all at run-time.

Therefore we somehow need to reflect the type level list at the term level: we need a value that corresponds exactly to the type. We do this by introducing a new type, indexed by a type level list, so that given a type level list of a particular length, our new type has exactly one value. Such a type—a type with exactly one value—is known as a singleton type:

data SList :: [k] -> Type where
  SNil  :: SList '[]
  SCons :: SList xs -> SList (x ': xs)

SList gives us a value that we can pattern match on, and when we do we discover something about the shape of the type level list xs:

mkNP' :: SList xs -> NP T xs
mkNP' SNil      = Nil
mkNP' (SCons s) = MkT 0 :* mkNP' s

The closest we can come to mkNP is to make this singleton value implicit:

class SListI (xs :: [k]) where
  sList :: SList xs

mkNP :: SListI xs => NP T xs
mkNP = mkNP' sList

If we now try to use mkNP to construct a value of our record

r0 :: R
r0 = npToR mkNP

we will of course find that we need an instance of SListI for IndicesR. Our first instinct might be to write something like

instance SListI IndicesR where
  sList =
      SCons
    $ SCons
    $ SCons
    -- .. lots more ..
    $ SCons
    $ SCons
    $ SNil

but if we do that, we will soon discover that the compiled code is quadratic in size. We could have predicted that: it’s the same problem as in the “Types” section above, with ($) playing the role of (<*>). But even if we write it as

instance SListI IndicesR where
  sList =
    SCons (
    SCons (
    SCons (
    -- .. lots more ..
    SCons (
    SCons (
    SNil
    ))) {- .. lots more brackets .. -} ))

we’re still in trouble: each of those SCons applications has two type argument x and xs (the type level list of the tail). So with some type annotations, this code is

instance SListI IndicesR where
  sList =
    SCons @00 @'[01, 02, 03, .., 99] (
    SCons @01 @'[    02, 03, .., 99] (
    SCons @02 @'[        03, .., 99] (
    -- .. lots more ..
    SCons @98 @'[                99] (
    SCons @99 @'[                  ] (
    SNil
    ))) {- .. lots more brackets .. -} ))

So this code is again O(n²) in size (actually, the real code generated by ghc is much worse than this, due to the fact that SList is a GADT; after desugaring, the function has a total size of 15,352, and after the simplifier runs (in -O0) that expands to a whopping 46,151).

Experienced type-level Haskellers might be surprised that we’d try to write this SListI instance by hand. After all, the definition of a singleton type is that it is a type with only a single value, and so we should be able to just derive it automatically. Indeed we can:

instance SListI '[] where
  sList = SNil

instance SListI xs => SListI (x ': xs) where
  sList = SCons sList

Surely we should be good now, right? These definitions are small, and don’t deal with concrete large lists, and so we avoid quadratic code size. Right? Wrong.

Although it is true that the two instances for SListI are unproblematic, the moment that we use npToR mkNP, ghc needs to prove SListI '[00, 01, .. 99]. In other words, it must generate code that produces a dictionary for SListI [00, 01, .. 99]. Since SListI for (x ': xs) has a superclass constraint SListI xs, the dictionary for SListI [00, 01, .., 99] will have a field for the dictionary for SListI [01, .., 99], all the way down to the empty type level list. This means that ghc will generate 100 dictionaries; each of those dictionaries contains an SCons application with the same type annotation as in hand-written code above. This means that we still have code that is O(n²) in size.

Concrete examples

In the previous section we discussed the ways in which we might end up with accidentally quadratic code size. In this section we will consider some examples of code generated by specific libraries. We will start with GHC generics, which is actually a good example: it generates code of size O(n log n) rather than O(n²). After that we will discuss record-dot-preprocessor and generics-sop, both of which do generate code of O(n²) size.

GHC Generics

The goal of generic programming is to be able to write a single function that can be applied to values of lots of different types. Generics libraries such as GHC.Generics and generics-sop (discussed below) do this by translating the value to a representation type; since every type can be translated to only a handful of different representation types, it suffices to write a function over all of those representation types.

Here we will discuss a simplified form of GHC.Generics that still illustrates the same point. The generic representation of a record such as the one above is essentially just a large nested tuple. For the GHC library itself it does not actually matter terribly how this tuple is created; for example, this would work:

type family GHC_Rep (a :: Type) :: Type

type instance GHC_Rep R = (T 00, (T 01, (T02, ... (T98, T99))))

Although it would work, it would not be great from a code size perspective. Consider the function that would translate R to GHC_Rep R:

ghcTo :: R -> GHC_Rep R
ghcTo MkR{..} =
    (,) @(T 00) @(T 01, (T02, ... (T98, T99))) f00 (
    (,) @(T 01)        @(T02, ... (T98, T99))  f01 (
    (,) @(T 02)             @(... (T98, T99))  f02 (
    -- .. lots more ..
    (,) @(T 99)                         @(())  f99 (
    () ))))

This pattern is starting to get familiar at this point; with this representation, ghcTo would be O(n²) in size. Fortunately, GHC generics avoids this problem by instead generating a balanced representation, something like

type instance GHC_Rep R =
 ( ( ( ( ( ( T 00, ( T 01, T 02 ) )
         , ( T 03, ( T 04, T 05 ) )
         )
 -- .. lots more ..
         , ( ( T 46, T 47 )
           , ( T 48, T 49 )
   ) ) ) ) )
 , ( ( ( ( ( T 50, ( T 51, T 52 ) )
         , ( T 53, ( T 54, T 55 ) )
         )
 -- .. lots more ..
         , ( ( T 96, T 97 )
           , ( T 98, T 99 )
 ) ) ) ) ) )

With this representation, the number of branches is still the same, but in the translation function the type annotations are now halved in size at each branch, rather than reduced by 1:

ghcTo :: R -> GHC_Rep R
ghcTo MkR{..} =
  ( ( ( ( ( ( f00, ( f01, f02 ) )
          , ( f03 , ( f04, f05 ) )
          )
  -- .. lots more ..
          , ( ( f96, f97 )
            , ( f98, f99 )
  ) ) ) ) ) )

As a consequence, the size of this version, and the cost of GHC generics in general, is actually O(n log n) in the number of record fields, although the constant factor is reasonably high.

It is worth emphasizing how much better O(n log n) is than O(n²). Here is a plot of the cost of GHC generics (in terms of AST size: terms, types and coercions) as we vary the number of record fields from 100 fields to 1000 fields:

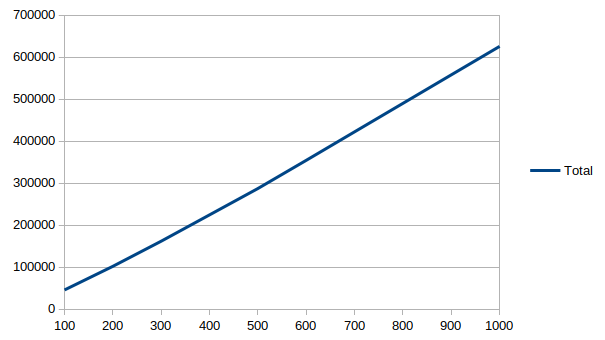
This almost looks linear. It isn’t; the cost per field is roughly 460 terms/types/coercions when we have 100 fields, and that increases to roughly 625 when we get to 1000 fields, but the cost only goes up very slowly.

The RecordDotSyntax preprocessor

The record-dot-preprocessor is a preprocessor and GHC plugin for the RecordDotSyntax GHC proposal. The preprocessor interprets specialized “record syntax”; for example, it translates

expr{lbl1.lbl2 = val}

to

setField @"lbl1" expr $ setField @"lbl2" (getField @"lbl1" expr) val

These two functions getField and hasField come from a HasField class currently provided by record-hasfield (although now that the Add setField to HasField proposal is accepted, this should eventually move to base):

class HasField x r a | x r -> a where
  hasField :: r -> (a -> r, a)

When you include

{-# OPTIONS_GHC -fplugin=RecordDotPreprocessor #-}

at the top of your Haskell file, the RecordDotPreprocessor plugin will generate HasField instances for you. They look innocuous enough:

instance HasField "f00" R (T 00) where
  hasField r = (\x -> r { f00 = x }, f00 r)

Unfortunately, once we get to ghc’s internal representation, this is much less innocent:

hasField_f00 :: R -> (T 0 -> R, T 0)
hasField_f00 r = (
      \new -> case r of
        MkR x00 x01 x02 x03 x04 x05 x06 x07 x08 x09
            x10 x11 x12 x13 x14 x15 x16 x17 x18 x19
            -- .. lots more ..
            x90 x91 x92 x93 x94 x95 x96 x97 x98 x99 ->
          MkR new x01 x02 x03 x04 x05 x06 x07 x08 x09
              x10 x11 x12 x13 x14 x15 x16 x17 x18 x19
              -- .. lots more ..
              x90 x91 x92 x93 x94 x95 x96 x97 x98 x99
    , case r of
        MkR x00 x01 x02 x03 x04 x05 x06 x07 x08 x09
            x10 x11 x12 x13 x14 x15 x16 x17 x18 x19
            -- .. lots more ..
            x90 x91 x92 x93 x94 x95 x96 x97 x98 x99 ->
          x00
    )

We saw this before when we discussed the record field accessors; the same linear cost that a field accessor induces is induced here as well, with a larger constant factor. As for field accessors, we need to generate a HasField instance for every field, and hence altogether we once again have code that is O(n²) in size.

This really matters: a module containing just the declaration of our record size has a total size of 22,065 terms/types/coercions after desugaring, and 22,277 after the simplifier (with -O0). This is already much bigger than it should be, due to the quadratic nature fo the field accessors. Generating HasField instances for all fields results in a total code size of 58,665 after desugaring and 78,977 after the simplifier. And all we’ve done is define the record! (For comparison, with large-records, a module containing a single record with 100 fields has a mere total size of 8,305 after desugaring, expanding to 13,958 after the simplifier, and that is including support for generics).

SOP generics

The generics-sop library is similar in nature to GHC generics, but it uses a different generic representation. It is described in detail in the paper True Sums of Products; here we give a simplified presentation.

In fact, we have already seen most ingredients. The generics-sop representation for a record is essentially the NP type that we discussed in “Type level induction”, above. In that section we saw that the function npToR that translates from the generic representation to R is linear in size. Unfortunately, the same is not true for the inverse function:

npFromR :: R -> NP T IndicesR
npFromR MkR{..} = (
       f00 :* f01 :* f02 :* f03 :* f04 :* f05 :* f06 :* f07 :* f08 :* f09
    :* f10 :* f11 :* f12 :* f13 :* f14 :* f15 :* f16 :* f17 :* f18 :* f19
    -- .. lots more ..
    :* f90 :* f91 :* f92 :* f93 :* f94 :* f95 :* f96 :* f97 :* f98 :* f99
#endif
    :* Nil
    )

That wildcard pattern match MkR{..} will expand to a pattern match for a variable for every field, but that doesn’t matter here: we only generate one translation function, and it’s fine if that is linear in size. The problem however is in the body of this function. After the previous examples, perhaps you can spot the problem already: (:*) has a bunch of type arguments, and one of those is the list of indices at the tail; so this code looks something like

npFromR MkR{..} =
    (:*) @00 @'[1, 2, .., 98, 99] f00 (
    (:*) @01 @'[   2, .., 98, 99] f01 (
    (:*) @02 @'[      .., 98, 99] f02 (
    -- .. lots more ..
    (:*) @98 @'[              99] f98 (
    (:*) @99 @'[                ] f99 (
    Nil )))))

a depressingly familiar sight at this point (and again, the real code is worse, due to the fact that NP is a GADT). This matters: the size of npToR is 4,441 terms/types/coercions, the size of npFromR is 46,459.

The generics-sop library suffers from quadratic code size in other places as well. It makes heavy use of type-level lists, in a similar style to SListI above, and with the same kinds of problems. It also represents metadata at the type-level, rather than just at the term level, which are more type-level lists. These are not fundamental problems; generics-sop simply wasn’t designed with the goal to optimize for code size reduction in mind. As we saw in the section on GHC generics, these costs can probably be brought down to O(n log n), though this will require careful thought.

The large-records library

When you use the large-records library and define

largeRecord defaultLazyOptions [d|
  data R = MkR {
      f00 :: T 00
    , f01 :: T 01
    , f02 :: T 02
    -- .. lots more ..
    , f98 :: T 98
    , f99 :: T 99
    }
  |]

You get the definition of a type R with field accessors, HasField instances for every field, and a Generic instance (albeit for a custom generics library), but the code will be entirely linear—O(n)—in the size of the record. In this section we will see how large-records achieves this for the basic definitions; we will discuss generics separately in the next section.

Representation

As we saw, the moment that we declare a record, ghc will generate field accessors for each field of the record, resulting in code that is O(n²) in size. It follows that we cannot use the normal representation of the record. Instead, large-records generates the following:

newtype R = LR__MkR { vectorFromR :: Vector Any }

That is, we are representing the record basically by an untyped vector which will have an entry for every field in the record.² Of course, typically users will never deal with this untyped representation directly, but use the field accessors or HasField instances, which we will discuss next.

Field accessors

Along with the definition of R, large-records generates an unsafe function that can return any element of the vector at any type:

unsafeGetIndexR :: Int -> R -> a
unsafeGetIndexR n t = noInlineUnsafeCo $ vectorFromR t n

where noInlineUnsafeCo is a non-inlinable form of unsafeCoerce³. Just like the internal representation of R, this function is not intended for normal use. Instead, it is used to define field accessors for each field. For example, here is the definition of the accessor f00:

f00 :: R -> T 0
f00 = unsafeGetIndexR 0

One of these accessors is generated for every field, but the size of each accessor is constant (and tiny), so the generation of all accessors results in code that is O(n) in size.

HasField instance

The HasField instance is very similar. Along with the unsafe accessor, we also define an unsafe update function:

unsafeSetIndexR :: Int -> R -> a -> R
unsafeSetIndexR n r x = LR__MkR $
    unsafeUpd (vectorFromR r) [(n, noInlineUnsafeCo x)]

The HasField instance is now easy, and once again constant in size and tiny:

instance HasField "f00" R (T 0) where
  hasField r = (unsafeSetIndexR 0 r, unsafeGetIndexR 0 r)

Pattern synonym

By default large-records does not generate a pattern synonym for R. It can do, if requested:

largeRecord (defaultLazyOptions {generatePatternSynonym = True}) [d|
  data R = MkR {
      f00 :: T 00
    , f01 :: T 01
    , f02 :: T 02
    -- .. lots more ..
    , f98 :: T 98
    , f99 :: T 99
    }
  |]

With the generatePatternSynonym option, large-records generates two new definitions. First, a function that constructs a tuple containing all fields of the record:

tupleFromR :: R
           -> ( (T 00, T 01, T 02, {- .. lots more .. -}, T 60, T 61)
              , (T 62, T 63, T 64, {- .. lots more .. -}, T 98, T 99)
              )
tupleFromR r = (
      unsafeGetIndexR 00 r
    , unsafeGetIndexR 01 r
    , unsafeGetIndexR 02 r
    -- .. lots more ..
    , unsafeGetIndexR 60 r
    , unsafeGetIndexR 61 r
    )
  , ( unsafeGetIndexR 62 r
    , unsafeGetIndexR 63 r
    , unsafeGetIndexR 64 r
     -- .. lots more ..
    , unsafeGetIndexR 98 r
    , unsafeGetIndexR 99 r
  ) )

(It was careful to use a nested tuple, because ghc does not support tuples with more than 62 fields.) It then uses this function as a view pattern in an explicitly bidirectional pattern synonym:

pattern MkR :: T 0 -> T 1 -> T 2 -> {- .. lots more .. -} -> T 98 -> T99 -> R
pattern MkR{f00, f01, f02, {- .. lots more .. -}, f98, f99} <-
    tupleFromR -> ( ( f00, f01, f02, f03, f04, f05, f06, f07, f08, f09
                    , f10, f11, f12, f13, f14, f15, f16, f17, f18, f19
                    -- .. lots more ..
                    , f60, f61
                    )
                  , (           f62, f63, f64, f65, f66, f67, f68, f69
                    -- .. lots more ..
                    , f90, f91, f92, f93, f94, f95, f96, f97, f98, f99
                  ) )
  where
    MkR x00 x01 x02 {- .. lots more .. -} x98 x99 = RFromVector $ fromList [
          unsafeCoerce x00
        , unsafeCoerce x01
        , unsafeCoerce x02
          -- .. lots more ..
        , unsafeCoerce x98
        , unsafeCoerce x99
        ]

The pattern synonym makes it possible to pattern match on R or construct R values as if it was defined in the normal way. The reason that we don’t generate it by default is an annoying one: when we declare a record pattern synonym, ghc very “helpfully” generates field accessors, which was precisely what we were trying to avoid.

So the option is there for code bases that need it; when enabled, we reintroduce a quadratic component, albeit a reasonably small one, and the rest of the generated code is still linear. Fortunately, many code bases that deal with large records never actually construct such records directly. They are instead populated from databases or from REST requests; in such cases, the pattern synonym is not required. In addition, large-records provides a quasi-quoter that can be used in lieu of the pattern synonym so that you can write, for example,

firstTwo :: R -> (T 0, T1)
firstTwo [lr| MkR { f00 = x0, f01 = x1 } |] = (x0, x1)

In ghc- 9.2 we have the new NoFieldSelectors language pragma (ghc proposal, merge request) which might improve the situation here, but I haven’t experimented with that yet.

Generics

The large-records library comes with its own Generic class. Although the class and its instances are defined rather differently, usage of the class—that is, the way you’d write generic functions—is very similar in style to generics-sop. The class is defined as

class Generic a where
  -- Translation
  from :: a -> Rep I a
  to   :: Rep I a -> a

  -- Constraints
  type Constraints a :: (Type -> Constraint) -> Constraint
  dict :: Constraints a c => Proxy c -> Rep (Dict c) a

  -- Metadata
  metadata :: Proxy a -> Metadata a

We will discuss the various parts of this class separately, and finish with an example of a generic function that ties all this together.

Translation to and from the generic representation

The generic representation used by large-records is

newtype Rep f a = Rep (Vector (f Any))

In other words, if we pick the identity functor for f, then Rep f a is just Vector Any; this means that from and to can just be coerce:⁴

instance Generic R where
  from = coerce
  to   = coerce
  -- .. more ..

Constraints

The Constraints type family is meant to capture the concept of “a constraint applied to all fields in the record”. We encountered this idea above in the section “Type class dictionaries”, where we noticed we have to be careful. Here is how large-records instantiates Constraints for our running example:

class Constraints_R c where
  dictConstraints_R :: Proxy c -> Rep (Dict c) R

instance Generic R where
  type Constraints R = Constraints_R
  dict = dictConstraints_R
  -- .. more ..

Constraints_R does not have any superclass constraints, thus avoiding the quadratic cost of all the dictionary projections. Instead, it is constructing a vector of dictionaries. Essentially, we are constructing our own representation of a dictionary, just like we constructed our own representation for a record. Unlike the GHC representation of dictionaries, we can project from our representation by just doing a vector index.

Fortunately, we can give an instance for Constraints_R:

instance ( c (T 0)
         , c (T 1)
         , c (T 2)
          -- .. lots more ..
         , c (T 98)
         , c (T 99)
         ) => Constraints_R c where
  dictConstraints_R p = Rep $ fromList [
        unsafeCoerce (dictFor p) (Proxy @(T 0))
      , unsafeCoerce (dictFor p) (Proxy @(T 1))
      , unsafeCoerce (dictFor p) (Proxy @(T 2))
      -- .. lots more ..
      , unsafeCoerce (dictFor p) (Proxy @(T 98))
      , unsafeCoerce (dictFor p) (Proxy @(T 99))
      ]

In core, this results in a single function with 100 arguments, that constructs our custom dictionary representation. This function is reasonably large (3523 terms/types/coercions), but not excessively so, and moreover, it is O(n) in the number of record fields.

Metadata

The Metadata provided by large-records is currently fairly minimal; it tells us the names of the record, its constructor, and the fields, as well as the strictness of each field:

data Metadata a = Metadata {
      recordName          :: String
    , recordConstructor   :: String
    , recordSize          :: Int
    , recordFieldMetadata :: Rep FieldMetadata a
    }

data FieldStrictness = FieldStrict | FieldLazy

data FieldMetadata x where
  FieldMetadata ::
       KnownSymbol name
    => Proxy name
    -> FieldStrictness
    -> FieldMetadata x

Metadata is generated automatically by the largeRecord invocation.

Note that the name of each field is at the type level; this is primarily to help with integration with GHC generics. This is essential for the integration of large-records with other libraries, but a detailed discussion of this is outside the scope of this blog post.

Writing generic functions

An in-depth discussion on how to write generic functions in the style of generics-sop is beyond the scope of this blog post; interested readers may wish to refer to the True Sums of Products paper or watch Andres Löh’s generics-sop tutorial at ZuriHac 2016 or read his SSGEP summer school lecture notes. Here we will discuss one (typical) example only.

Generic functions in generics-sop style are written using a set of combinators on the generic representation. As a simple example, we can zip two Reps:

zipWith :: (forall x. f x -> g x -> h x)
        -> Rep f a -> Rep g a -> Rep h a

It is worth spelling out what this function is doing: it is zipping together all the fields of two records, albeit in their generic representation (Rep). We therefore require that the function we’re zipping with is polymorphic: we must be able to zip fields no matter their type.

As another example, we can map a function over all fields in the record; there is a function map, as you’d expect:

map :: (forall x. f x -> g x) -> Rep f a -> Rep g a

but there is also a slightly more useful version of this:

cmap :: (Generic a, Constraints a c)
     => Proxy c
     -> (forall x. c x => f x -> g x)
     -> Rep f a -> Rep g a

This constrained map still requires the function we’re applying to all fields to be polymorphic, but it is given the guarantee that the types it is applied to all satisfy constraint c. Of course, in order to be able to do that, we need constraint c to hold for all fields, which is why this function requires Constraints a c. There is a similar generalization of zipWith called czipWith, as well as applicative versions of both of these functions.

The final combinator we will discuss applies when we have a vector in which every element has the same type: in this case, we can collapse the vector to an ordinary list:

collapse :: Rep (K a) b -> [a]

Here is an example of a generic function that can translate any value to JSON, provided it has a Generic instance and provided we have ToJSON instances for all fields:

gtoJSON :: forall a. (Generic a, Constraints a ToJSON) => a -> Value
gtoJSON =
      Aeson.object
    . Rep.collapse
    . Rep.zipWith (mapKKK $ \n x -> (Text.pack n, x)) recordFieldNames
    . Rep.cmap (Proxy @ToJSON) (K . toJSON . unI)
    . from
  where
    Metadata{..} = metadata (Proxy @a)

If you are new to generics-sop style programming, this function may require careful reading, but the essence of it is simple:

1. Translate the value to its generic representation using from
2. Apply toJSON to all fields
3. Zip it with the metadata to get a vector of (name, value) pairs
4. Collapse that vector to a list
5. Use Aeson’s standard object function to create the JSON object.

Once you are used to the paradigm, generics-sop style programming allows for the very succinct definition of generic functions (I’d go so far as calling it “elegant”, but then I am biased). Typically a function like gtoJSON would be used to derive a ToJSON instance:

instance ToJSON R where
  toJSON = gtoJSON

Indeed, the large-records library can generate such instances automatically for a handful of classes.

Transforms

The only aspect of the generics programming aspect of large-records we have not covered here is what is known as “transforms” in generics-sop style programming. Transforms allow you to generically modify type indices; for example, suppose we have a HKD-style definition of a table, as used in the beam database library:

data Table f = MkTable {
      tableField1 :: f Int
    , tableField2 :: f Maybe
    }

We could write a generic function that could, say, turn a Table Identity into a Table Maybe. Doing this without using type-level lists anywhere is surprisingly difficult, and a discussion of how this is done in large-records is probably a good topic for a separate blog post. For now we just refer any interested readers to the examples in the test suite.

Talking of beam, large-records integrates smoothly with beam-core by means of an auxiliary library beam-large-records. This library is on GitHub but is not available on Hackage yet because it depends on a small patch to beam. Hopefully it will be released soon.

Benchmarks

For the purpose of these benchmarks, we are interested in compile-time, not run-time performance. I have not yet done any benchmarks of run-time performance. There might be some run-time benefits compared to other generics approaches because there is no conversion to and from a generic representation, but there are probably some performance penalties for normal functions because the record representation used internally in large-records is much less transparent to the GHC optimizer. Measuring this is future work.

In terms of compile time performance, however, the results are pretty clear. Here is a graph of the size of the core AST of the module (the sum of the terms, types and coercions in the module) plotted against the number of record fields, after desugaring:

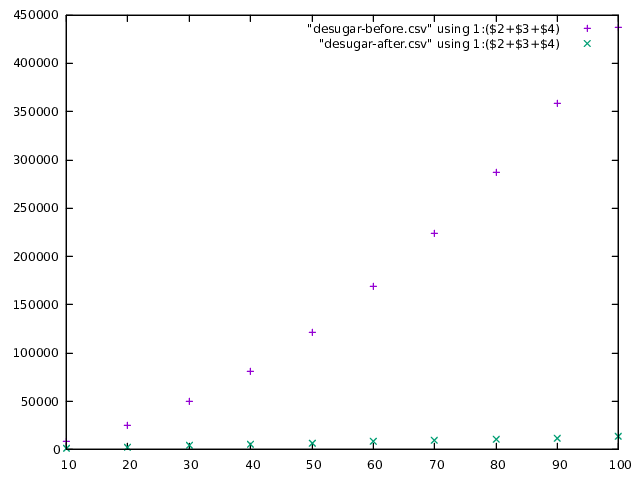
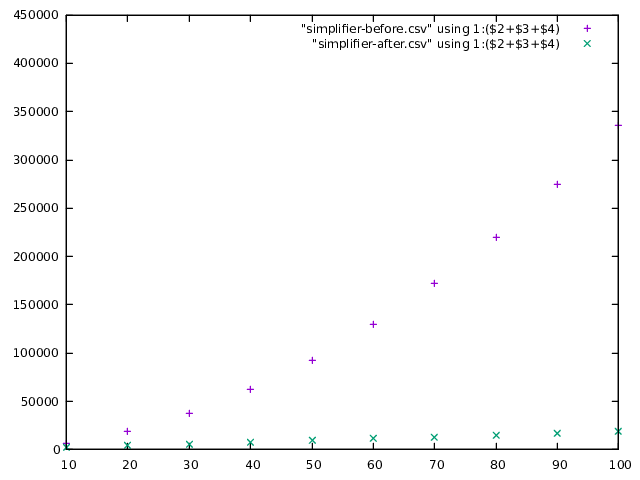
As you can see, for vanilla ghc the size grows quadratically to nearly 450,000 nodes, but stays nice and flat for large-records. The GHC simplifier reduces the size of the AST a bit in the case of vanilla ghc and increases it a bit for large-records, but large-records is still the clear winner:

In terms of “real” performance measurements, here is a plot of ghc memory usage as reported by the OS (in kB), against the number of record fields:

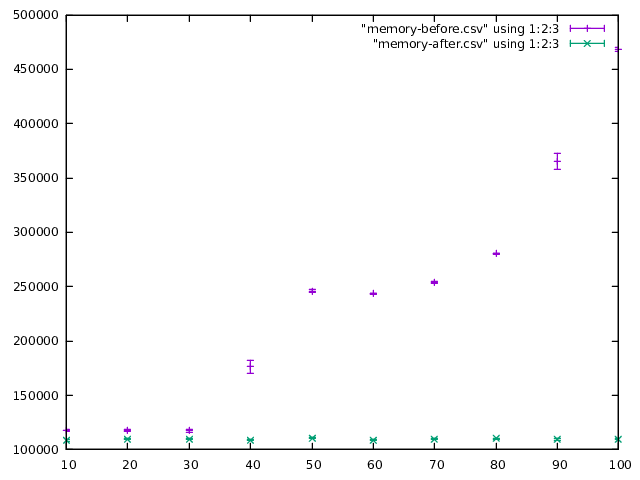
As you can see, ghc climbs to roughly 500 MB for 100 fields, whereas large-records stays near the 100 MB mark. There is a similar graph for compilation time (in terms of elapsed wall-clock time in seconds):

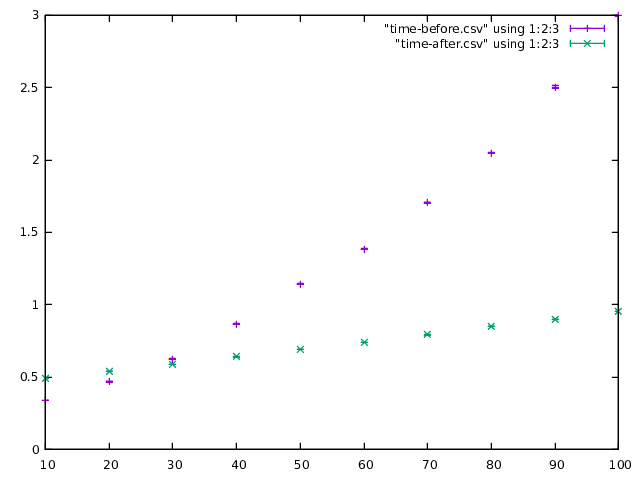
For vanilla ghc compilation takes roughly 3 seconds for 100 fields, whereas large-records is 3x times faster and stays under one second.

(These numbers have been normalized against compiling an empty module. The error bars here indicate standard error; each module has been compiled 100 times.)

Conclusions

The large-records library generates code that is strictly O(n) in size in the number of record fields. It does so at the cost of generating basically untyped core. This does not matter for code using large-records, which is still presented with a perfectly safe, typed interface. It might however reduce the applicability of the techniques employed by large-records more generally within ghc: the History of Haskell paper (Section 9.1) emphasizes the importance of having a typed internal ghc language to catch and help debug compiler bugs.

Perhaps aiming for linear cost however is not necessary. We saw in the section on GHC generics that if we are careful how we set things up, we can generate code that is O(n log n) in size. Similar techniques can be applied in libraries such as generics-sop as well, provided that we are careful at every step; for example, the use of type-level lists should be avoided and we should be using type-level (balanced) trees instead.

In order to tackle the problem at a more fundamental level, we might need to be able to introduce and control sharing at the type level; Richard Eisenberg opened ghc ticket #20264 after my HIW talk on large-records with some thoughts on the topic. As a completely alternative approach, the work on Scrap your type applications removes type arguments altogether. This may well address many of the concerns in this blog post, but it’s such a radically different internal language that it’s hard to foresee quite all the consequences.

Addressing the overabundance with types is however only one aspect of the problem, albeit an important one. Specifically, it does not prevent record pattern matches and record updates (either on term level records or on type class dictionaries) in core always being linear in the size of the record. Perhaps an extension to core could alleviate this problem, though changes to core affect to the entire compiler backend and so are rightly treated with extreme prejudice.

When such problems are addressed in ghc, a library like large-records may no longer be required. Until such time, however, the large-records library can be used to significantly reduce compile time and memory requirements for code bases that contain many large records.