Type-level sharing in Haskell, now

The lack of type-level sharing in Haskell is a long-standing problem. It means, for example, that this simple Haskell code

apBaseline :: Applicative f => (A -> B -> C -> r) -> f r
apBaseline f =
        pure f
    <*> pure A
    <*> pure B
    <*> pure C

results in core code that is quadratic in size, due to type arguments; in pseudo-Haskell, it will look something like

apBaseline :: Applicative f => (A -> B -> C -> r) -> f r
apBaseline f =
                          (pure f)
    <*> @A @(B -> C -> r) (pure A)
    <*> @B @(     C -> r) (pure B)
    <*> @C @(          r) (pure C)

Each application of (<*>) records both the type of the argument that we are applying, as well as the types of all remaining arguments. Since the latter is linear in the number of arguments, and we have a linear number of applications of <*>, the core size of this function becomes quadratic in the number of arguments.

We recently discovered a way to solve this problem, in ghc as it is today (tested with 8.8, 8.10, 9.0 and 9.2). In this blog post we will describe the approach, as well as introduce a new typechecker plugin (available from Hackage or GitHub) which makes the process more convenient.

It is exciting that we now have an answer to a previously unsolved problem, but it must be admitted that the resulting code is not very elegant, and fairly unpleasant to write. It will be necessary to explore this new approach, find new ways to use it and adapt it to improve the user experience. We are nonetheless releasing this blog post, and the plugin, in the hope that others might feel inspired to experiment with it and devise new ways in which it can be used.

Vanilla ghc

Before we introduce the new typechecker plugin, we will first demonstrate the concept in vanilla ghc. Here’s the main idea: we will represent a type-level let-binding as an existentially quantified type variable, along with an equality that specifies the value of that variable; the equality will be opaque to ghc until we reveal it.

That probably sounds rather abstract, so let’s make this more concrete:

data a :~: b where             -- defined in base (Data.Type.Equality)
  Refl :: a :~: a

data LetT :: a -> Type where   -- new
  LetT :: (b :~: a) -> LetT a

The LetT constructor has two type variables, a and b; b is the existential type variable mentioned above, while a is a regular type variable, and will correspond to the value of the type variable we are “let-binding”. In other words, think of this as a type-level assignment b := a. The argument b :~: a records the equality between a and b; it is opaque to ghc in the sense that ghc will not be aware of this equality until we pattern match on the Refl constructor.

When we construct a let-binding, a and b will (by definition) have the same value, and so we can introduce a helper function:

{-# NOINLINE letT #-}
letT :: LetT a
letT = LetT Refl

This gives us a let-binding with value a, for an existential variable that we will discover when we pattern match on the LetT constructor.¹

This is all probably still quite abstract, so let’s see a simple example of how we might use this:

castSingleLet :: Int -> Int
castSingleLet x =
    case letT of { LetT (p :: b :~: Int) ->   -- (1)
      let x' :: b
          x' = case p of Refl -> x            -- (2)
      in case p of Refl -> x'                 -- (3)
    }

In (1), we introduce a type-level let-binding b := Int. Then in (2) we define a value x' of type b; we know that b := Int, but ghc doesn’t, and so we explicitly pattern match on the equality proof. Finally, in (3) we want to use x' as the result of the function; for this we need to cast back from b to Int.

Of course, this example is a bit pointless, so let’s consider how we might actually use this to solve a problem.

Heterogenous lists

We will come back to the applicative example from the introduction a bit later, but let’s consider a slightly simpler example first. Recall this definition of heterogenous lists:

data HList :: [Type] -> Type where
  HNil  :: HList '[]
  HCons :: x -> HList xs -> HList (x : xs)

Without type-level sharing, we cannot construct values of type HList without resulting in quadratic core code size, for much the same reason as before. For example,

hlistBaseline :: HList '[A, B, C]
hlistBaseline =
      HCons A
    $ HCons B
    $ HCons C
    $ HNil

will be expanded with type variables to something like

hlistBaseline :: HList '[A, B, C]
hlistBaseline =
      HCons @'[A, B, C] A
    $ HCons @'[   B, C] B
    $ HCons @'[      C]
    $ HNil

where we again have a linear number of calls to HCons, each of which has a list of type arguments which is itself linear; hence, this value is quadratic in size.

Let’s fix that. Instead of repeating the list each time, we will introduce type-level sharing so that we can express, “this list is like that other list over there, but with an additional value at the front”. Let’s first define the various type-level lists:

hlist1 :: HList '[A, B, C]
hlist1 =
   case letT of { LetT (p2 :: r2 :~: (C : '[])) ->   -- r2 := C : []
   case letT of { LetT (p1 :: r1 :~: (B : r2 )) ->   -- r1 := B : r2
   case letT of { LetT (p0 :: r0 :~: (A : r1 )) ->   -- r0 := A : r1
     ...
   }}}

With the type-level lists defined, we can now define the corresponding values. Just like before, we need to cast explicitly. For example, the list HCons C HNil has type HList (C : '[]); we know that this is the same as HList r2, but to convince ghc of that fact, we need to appeal to the explicit equality.

let xs2 :: HList r2
    xs1 :: HList r1
    xs0 :: HList r0

    xs2 = case p2 of Refl -> HCons C HNil
    xs1 = case p1 of Refl -> HCons B xs2
    xs0 = case p0 of Refl -> HCons A xs1

Finally, we need to cast back from HList r0 to HList '[A, B, C]; we will need to appeal to all equalities in order to do so. The full function is:

hlist1 :: HList '[A, B, C]
hlist1 =
   case letT of { LetT (p2 :: r2 :~: (C : '[])) ->
   case letT of { LetT (p1 :: r1 :~: (B : r2 )) ->
   case letT of { LetT (p0 :: r0 :~: (A : r1 )) ->

     let xs2 :: HList r2
         xs1 :: HList r1
         xs0 :: HList r0

         xs2 = case p2 of Refl -> HCons C HNil
         xs1 = case p1 of Refl -> HCons B xs2
         xs0 = case p0 of Refl -> HCons A xs1

     in case p0 of { Refl ->
        case p1 of { Refl ->
        case p2 of { Refl ->
          xs0
        }}}

   }}}

Unpacking equalities

It is critical that ghc cannot see the equalities we introduce, because if it did, it would just unfold the definition and we’d lose the sharing we worked so hard to introduce. Nonetheless, the need to match on all these equality proofs in order to cast values to the right type is certainly inconvenient. It is also easy to get wrong; we will discuss that problems in this section, but fortunately we can avoid the need for pattern matching altogether when we use the typelet type checker plugin; we will introduce this plugin in the next section.

The reason that the pattern matches are easy to get wrong is that we need to match in the right order. Concretely, if instead of the order above, we instead did

case p2 of { Refl ->
case p1 of { Refl ->
case p0 of { Refl ->
  xs0
}}}

we would end up with quadratic code again.

This is due to the shape of the equality proof that ghc constructs: xs0 has type HList r0, but we want to use it at type HList '[A, B, C]. There are sufficient equalities in scope to enable ghc to prove that these two types are in fact the same, which is why the program is accepted, but the resulting core code will look like

   xs0 `cast` {- .. proof that HList r0 ~ HList '[A, B, C] .. -}

In the linear version (where we pattern match on p0 first), we end up with the proof

let co2 :: r2 ~ (C : [])
    co1 :: r1 ~ (B : r2)
    co0 :: r0 ~ (A : r1)

    co2 = ..
    co1 = ..
    co0 = ..

in .. co2 .. co1 .. co0 ..

which mirrors our own definitions very closely. However, if we match in the wrong order, we get this proof instead:

let co2 :: r2 ~ '[      C]
    co1 :: r1 ~ '[   B, C]
    co0 :: r0 ~ '[A, B, C]

    co2 = ..
    co1 = .. co2 ..
    co0 = .. co1 ..

in .. co0 ..

When we unpack the equalities in the right order, ghc first learns that r0 ~ (A : r1), without yet knowing what r1 is, and so it just constructs a proof for that; similarly, on the next equality, it learns that r1 ~ (B : r2), without knowing what r2 is, and so it constructs the corresponding proof (without modifying the proof it generated previously). When we do things in the opposite order, ghc first learns that r2 ~ (C : '[]); then when it learns that r1 ~ (B : r2), it already knows what r2 is, and so it constructs a proof for r1 ~ (B : C), and we have lost sharing.

Of course, we don’t really want these proofs at all, and indeed, when we use the plugin, we won’t get them.

The typelet typechecker plugin

To use the typelet typechecker plugin, just add

{-# OPTIONS_GHC -fplugin=TypeLet #-}

at the top of your module. When we use type plugin, we can write the HList example as

hlistLet :: HList '[A, B, C]
hlistLet =
    case letT (Proxy @(C : '[])) of { LetT (_ :: Proxy r2) ->
    case letT (Proxy @(B : r2))  of { LetT (_ :: Proxy r1) ->
    case letT (Proxy @(A : r1))  of { LetT (_ :: Proxy r0) ->

     let xs2 :: HList r2
         xs1 :: HList r1
         xs0 :: HList r0

         xs2 = castEqual (HCons C HNil)
         xs1 = castEqual (HCons B xs2)
         xs0 = castEqual (HCons A xs1)

     in castEqual xs0
    }}}

We still need to be explicit about when we want to cast, but we don’t need to be explicit anymore about how we want to cast. As an additional bonus, the resulting core code also doesn’t have any coercion proofs. (We will see below how we can rewrite this example more compactly using another combinator from the library.)

In the remainder of this blog post we will discuss the type system extension provided by the plugin. We will not discuss how it works internally; it is a reasonably simple type checker plugin and a discussion of the implementation is not relevant for our goal here, which is type-level sharing.

Let and Equal

The typelet library introduces two new classes, Let and Equal. Let is defined as

class Let (a :: k) (b :: k)

A constraint Let x t, where x is an existentially bound type variable, models a type-level let-bnding x := t. Only constraints of this shape (with x a variable²) are valid, and let-bindings cannot be recursive; if either of these conditions are not met, the plugin will emit a type error.

Let has a single instance for reflexivity (much like the use of Refl in letT above):

instance Let a a

In order to introduce the existential type variable, we define a LetT type much like we did above, but now carrying evidence of a Let constraint:

data LetT (a :: k) where
  LetT :: Let b a => Proxy b -> LetT a

letT :: Proxy a -> LetT a
letT p = LetT p

Of course, introducing let bindings is only one half of the story. We must also be able to apply them. This is where the second class, Equal, comes in:

class Equal (a :: k) (b :: k)

castEqual :: Equal a b => a -> b
castEqual = unsafeCoerce

Equal is a class without any instances; constraints Equal a b are instead solved by the plugin. Function castEqual allows to coerce from a to b whenever the plugin can prove that a and b are equal³. Formally:

In order words, the Let constraints define an (idempotent) substitution, and an Equal a b constraint is solvable whenever a and b are nominally equal types after applying that substitution.

For a trivial example, two types that are already nominally equal will also be Equal:

castReflexive :: Int -> Int
castReflexive = castEqual

The following example is slightly more interesting, and is the equivalent of castSingleLet that we already saw above, but now using the plugin:

castSingleLet :: Int -> Int
castSingleLet x =
    case letT (Proxy @Int) of
      LetT (_ :: Proxy t1) ->
        let y :: t1
            y = castEqual x
        in castEqual y

We saw a more realistic example above, in the definition of hlistLet.

Combining a type-level let with a cast

In castSingleLet we define a type variable t1, and then immediately cast a value to that type. That is such a common idiom that the typelet library provides a custom combinator for it:

data LetAs f (a :: k) where
  LetAs :: Let b a => f b -> LetAs f a

letAs :: f a -> LetAs f a
letAs x = LetAs x

Most of the time, we don’t want to hide the entire type of some value, because then that value would become unuseable without a cast (we’d have no information about its type). That’s why LetAs is parameterised by some functor f; when we have a value of type f a, letAs introduces a let-binding b := a, and then casts the value to f b. Here is a simple example:

castSingleLetAs :: Identity Int -> Identity Int
castSingleLetAs x =
    case letAs x of
      LetAs (x' :: Identity t1) ->
        castEqual x'

For a more realistic example, let’s consider the HList example once more. Here too we see the same idiom: we introduce a type-level let binding for the type-level list, and then cast a term-level value. Using letAs we can do that in one go:

hlistLetAs :: HList '[A, B, C]
hlistLetAs =
    case letAs (HCons C HNil) of { LetAs (xs02 :: HList t02) ->
    case letAs (HCons B xs02) of { LetAs (xs01 :: HList t01) ->
    case letAs (HCons A xs01) of { LetAs (xs00 :: HList t00) ->
      castEqual xs00
    }}}

CPS

Both letT and letAs introduce a data constructor, only for us to then directly pattern match on it again. The obvious question then is whether we might be able to avoid this using CPS form. Indeed we can, but we do have to be careful. The library defines CPS forms of both letT and letAs:

letT' :: forall r a. Proxy a -> (forall b. Let b a => Proxy b -> r) -> r
letT' pa k = case letT pa of LetT pb -> k pb

letAs' :: forall r f a. f a -> (forall b. Let b a => f b -> r) -> r
letAs' fa k = case letAs fa of LetAs fb -> k fb

The problem is that these abstractions introduce a type variable for the continuation (r), which may itself require sharing. The “obvious but wrong” translation of hlistLetAs, above, is

hlistLetAsCPS_bad :: HList '[A, B, C]
hlistLetAsCPS_bad =
    letAs' (HCons C HNil) $ \(xs02 :: HList t02) ->
    letAs' (HCons B xs02) $ \(xs01 :: HList t01) ->
    letAs' (HCons A xs01) $ \(xs00 :: HList t00) ->
      castEqual xs00

This is wrong, because the continuation variable r for each call to letAs' is HList '[A, B, C]: the type of the final result. But this means that we have n occurrences of the full n elements of the list, and so we are back to code that is O(n²) in size. If we do want to use CPS form, we have to introduce one additional let binding for the final result:

hlistLetAsCPS :: HList '[A, B, C]
hlistLetAsCPS =
    letT' (Proxy @'[A, B, C]) $ \(_ :: Proxy r) -> castEqual $
      letAs' @(HList r) (HCons C HNil) $ \(xs02 :: HList t02) ->
      letAs' @(HList r) (HCons B xs02) $ \(xs01 :: HList t01) ->
      letAs' @(HList r) (HCons A xs01) $ \(xs00 :: HList t00) ->
        castEqual xs00

Applicative

For the HList example, we can give a type-level let for the tail of the list (C ': []), and at the same type provide a value of that type. The fact that we do things “in the same order” at the type level is what made it possible to use the letAs combinator.

Unfortunately, that is not always the case. For example, in the applicative chain example from the introduction the order doesn’t quite work out: we must give type-level let bindings starting at the end

l02 := C -> r
l01 := B -> l01
l00 := A -> l00

but we need to apply arguments in the reverse order (A, then B, then C). Put another way, associativity at the type-level and at the term-level match for the HList example (both right-associative), but mismatch for the applicative example (right associative for the function type and left associative for function application).

Perhaps we will discover further combinators that help with this example, but for now it means that we need to use the more verbose option to write the function:

apLet :: forall f r. Applicative f => (A -> B -> C -> r) -> f r
apLet f =
    case letT (Proxy @(C -> r))   of { LetT (_ :: Proxy l02) ->
    case letT (Proxy @(B -> l02)) of { LetT (_ :: Proxy l01) ->
    case letT (Proxy @(A -> l01)) of { LetT (_ :: Proxy l00) ->

      let f00 :: f l00
          f01 :: f l01
          f02 :: f l02

          res :: f r

          f00 = pure (castEqual f)
          f01 = castEqual f00 <*> pure A
          f02 = castEqual f01 <*> pure B
          res = castEqual f02 <*> pure C

      in res

    }}}

Benchmarks

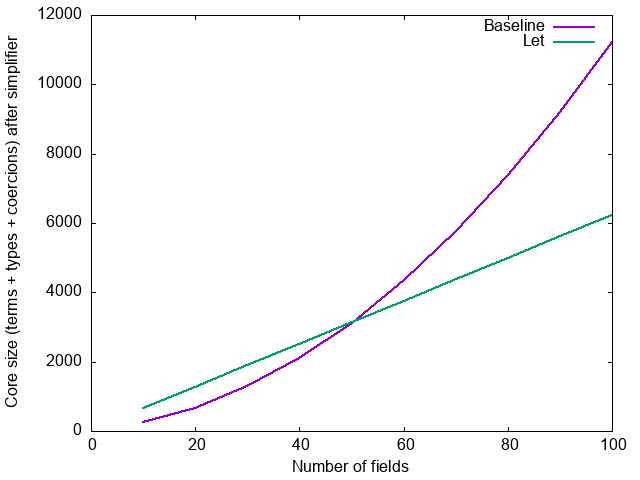
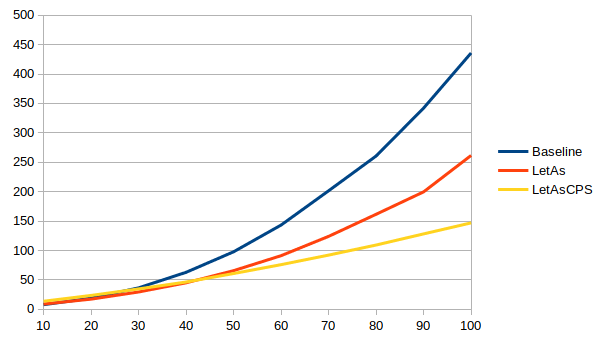
Is all this really worth it? It depends. For the applicative chain, the difference is not huge, and the let-bindings add some overhead:

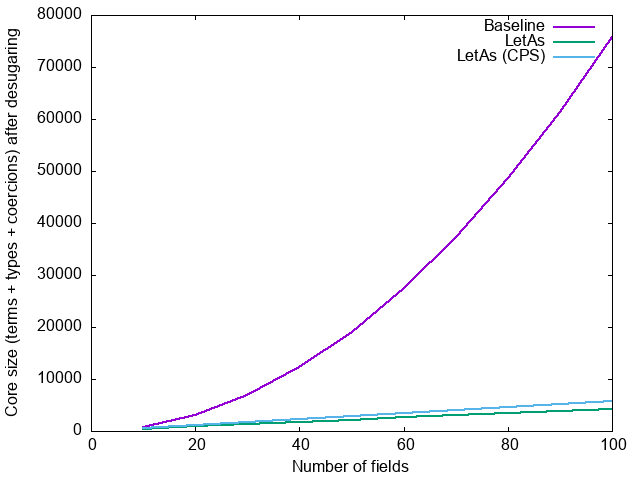
For GADTs, however, the difference is much more dramatic. For the HList example, after desugaring:

and after the simplifier:

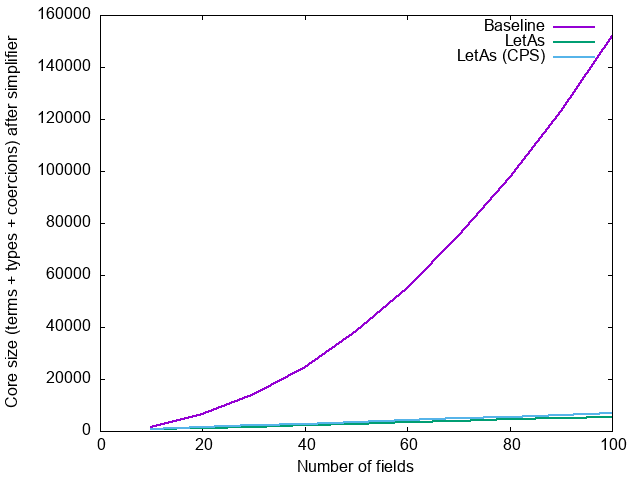
This is all with -O0; the primary goal here is to optimize compilation time during development. Talking of compilation time, let’s measure that too. Unfortunately, the performance of the HList example using letAs (rather than the CPS version) depends critically on the performance of ghc’s pattern match exhaustiveness checker, which differs quite a bit between ghc versions. Let’s first disable that altogether:

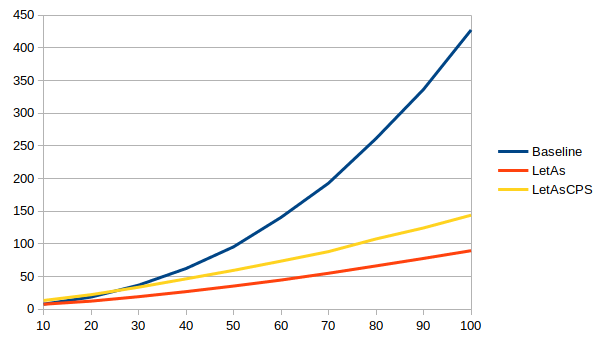
-Wno-incomplete-patterns -Wno-incomplete-uni-patterns -Wno-overlapping-patterns

With these options, compilation time for the three HList variations (baseline without sharing, letAs, and the CPS version letAs') are similar across ghc 8.8, 8.10, 9.0 and 9.2, and look something like (compilation time in ms versus number of entries in the list):

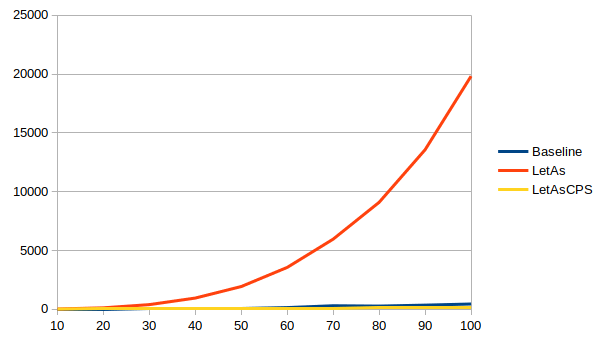
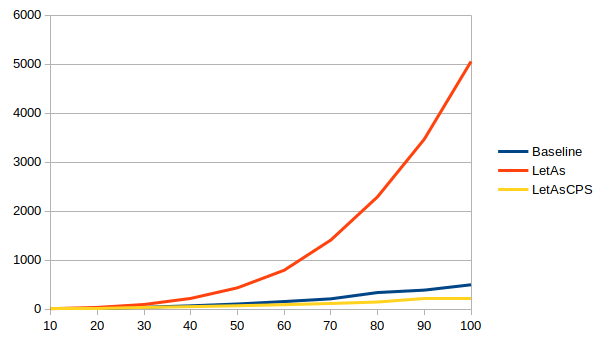
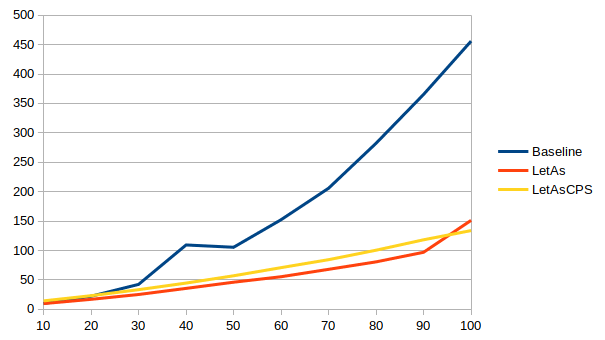
With the exhaustiveness checker enabled, times vary wildly between ghc versions for the non-CPS version (note: these graphs have different ranges on their y-axes):

8.8	8.10
9.0	9.2

The non-CPS version is up to 1.6x faster than the baseline in 8.8, but up to 44x slower in 8.10. The situation improves a bit in 9.0, but it’s still up to 10x slower than the baseline, until sanity is restored in 9.2 and the non-CPS version is up to 3x faster than the baseline.

The CPS version meanwhile is more stable across versions: up to 3x faster in 8.8 and 8.10, a slightly less impressive improvement of up to 2.4x faster in 9.0, and then back to up to 3.4x faster in 9.2.

Conclusions

The typelet type checker plugin offers an API that makes it possible to introduce type-level sharing in ghc as it is today (tested with 8.8, 8.10, 9.0 and 9.2). This is pretty exciting, but like any new abstraction, we need to experiment with it to discover the best way it can be used. We are releasing the plugin as well as this blog post at this early stage in the hope that others will feel inspired to try it and share their discoveries.

Our own motivation for developing this now is our continued efforts on behalf of Juspay to improve their compile times. In particular, we are currently looking at how we could support large anonymous records that compile in less-than-quadratic core space. Of course, type level sharing is only one weapon in our arsenal if we want to optimize for compilation time; my previous two blog posts in this series (Avoiding quadratic core code size with large records and Induction without core-size blow-up) discuss many others, and the search is not yet over.