We previously talked about the cabal solver and the qualified goals extension. In that blog post we briefly mentioned that failure nodes record conflict sets. In this blog post we take a closer look at these conflict sets and discuss how they are constructed and used.
Recap: search trees
Consider a package database where we have two versions of package A available: A-1.0 depends on B-1.0, and A-2.0 depends on B-2.0. However, only version 1.0 of package B is available. We will write this as follows:
A-1.0 => B-1.0A-2.0 => B-2.0B-1.0
When we ask the solver to pick a version for A, it constructs a search tree that looks like this:
(ANDRES: Why do the pictures need the extra digit in each of the versions? Just unnecessary noise.)
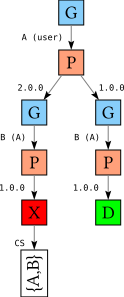
As you might recall from the previous blog post, a tree like this starts with a G (GoalChoice) node, choosing a goal to solve for next. In this case, there isn’t really a choice: we have to solve for the user-specified goal (A). We always write the immediate reason for introducing a goal in parentheses, so A (user) in the tree means that A is indeed a user-specified goals.
After that we have a P (PChoice) node, choosing a version for A. In the left branch we choose version 2.0, in the right branch we choose version 1.0. No matter which version we choose, we then have to solve for goal B (second G node), because B is a dependency of A. There is only one version of B available, version 1.0 (second P node). The left branch leads to failure (an X node), and the right branch leads to success (a D node).
Conflict sets
Let’s now focus on the failure in the above tree.
Constrained instances
The search tree gets built in a number of separate steps. In the first step, we just enumerate all possibilities, without verifying which of those possibilities are actually valid solutions. For our example, this looks like
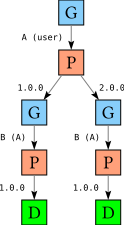
This tree is then validated. As part of validation we associate with every package a constrained instance (CI). A constrained instance is either a particular choice of version or else a range of acceptable versions, paired with a reason why the version was constrained in that way.
In the example, once we pick version 2.0 for A
- the constrained instance for
Abecomes a fixed choice (2.0), - the constrained instance for
Brecords that the version ofBmust be 2.0, and that this requirement comes fromA.
Then when we pick version 1.0 of B, we detect a conflict; in this case, a conflict between the choice we just made for B, and the fact that the instance for B was previously constrained by A. A conflict means that we failed to find a solution in this path of the tree; this is recorded as an X (Fail) node in the tree, and we additionally record the conflict set as part of the failure, ending up with the tree as we saw it before:

The conflict set records which set of choices are in conflict with each other; in this case, it’s the choice for A and the choice for B.
Irrelevant choices
When the solver looks for a solution, it does a depth-first search of this tree, so it will explore the left branch first. In this branch we pick version 2.0 of A, which relies on version 2.0 of B, which is unavailable: this path leads to failure.
When the solver finds an X (Fail) node, it must backtrack and reconsider the choices it made. The conservative (but slow) approach would be to simply reconsider every choice we made. However, this is not always necessary; consider the following variation on the above problem: we still have two versions of A, and A-1.0 still depends on B-1.0 while A-2.0 still depends on B-2.0, which is unavailable. However, A-2.0 now additionally depends on (any version of) C, for which we have two versions available, C-1.0 and C-2.0:
A-1.0 => B-1.0A-2.0 => B-2.0, C-*B-1.0C-1.0C-2.0
If we now ask the solver to find a solution for A, it constructs the following search tree:
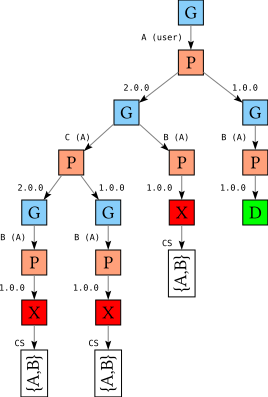
This tree is a little larger than the previous because once we choose version 2.0 for A, we can choose to solve for B first or solve for C first, and when we solve for C we have two choices of versions. Let’s concentrate on the left-most path through this tree:
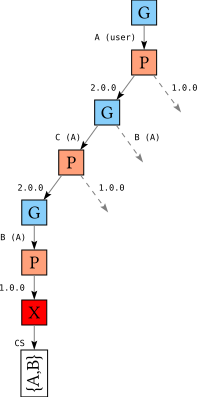
We choose to solve for A first, pick version A-2.0, then choose to solve for C, pick version C-2.0, and finally solve for B, picking version B-1.0 before realizing that actually this does not lead to a valid solution. However, now when we start backtracking and reconsider some of the choices we made, there is no point reconsidering the choice for C: the conflict was between packages A and B, so unless we make a different choice for either of those two packages we will not find a solution.
The solver takes advantage of this fact and (almost) only reconsiders choices that were recorded as part of the conflict set.
Source of the conflict
Hopefully the previous two sections made it clear why the conflict set for the conflict we are considering must include A, and does not need to include some unrelated package C. What might not be completely obvious is why it needs to include B. After all, making a different choice for B will not help!
However, when we discover a conflict between packages A and B we cannot in general know whether we should make a different choice for A or for B. After all, the database could have looked like this instead:
A-1.0 => B-1.0B-1.0B-2.0
with corresponding search tree:
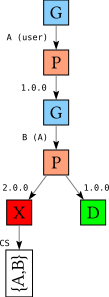
In this case, when we reach the conflict, we need to make a different choice for B instead.
To summarize, when we reach a conflict, all packages involved in the conflict should be recorded as part of the conflict set:

|

|

|
| We need A .. | .. and B .. | .. but not C |
|---|
More examples
We will discuss a few more examples of how conflicts arise in the search tree and what the corresponding conflict sets are.
Cycles
Consider the following database:
A.1.0 => B-*B-1.0B-2.0 => C-*C-1.0 => A-*
Choosing version 2.0 for B leads to a cycle (A => B => C => A), so we must choose version 1.0:
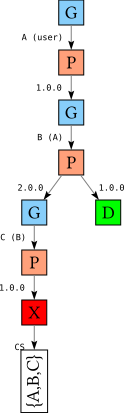
A cycle is a conflict between the choices for all packages involved in the cycle; after all, we don’t know for which package we should make a different choice. In this example it is B, but we could just as easily have constructed an example where it was A or C, or indeed multiple. Thus, the conflict set records all packages in the cycle.
Single instance restriction
Consider the database
A-1.0 => C-*B-1.0 => C-*C-1.0
Suppose we ask the solver to solve for A and B as independent goals (for a discussion of independent goals the the previous blog about the cabal solver and the qualified goals extension); the constructed search tree is relatively large, so let’s focus on section of it:
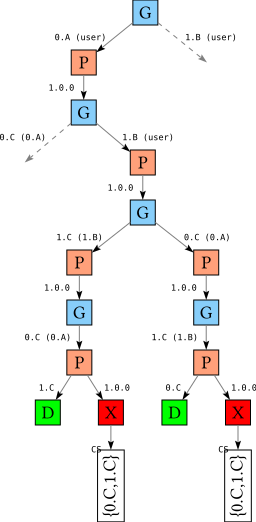
In this fragment we choose to solve for A first, and then for B. Since A and B are independent goals, they have been given a different qualifiers 0.A and 1.B, which means we subsequently have two goals left to solve for: the dependency 0.C of A on C, and the dependency 1.C of B on C.
In the left subtree, we choose to solve for 1.C first, and we pick version 1.0 (it’s the only choice); remains to solve for 0.C. At this point we have two possibilities: we can choose to link 1.C against 0.C (in other words, use the very same copy of C for B that we used for A), or we can choose to build a separate copy of C just for B.
However, at the moment GHC still imposes the single instance restriction, which means that we cannot install more than one copy of one package version. From the solver’s point of view, this means that there can be at most one qualified goal that resolves to a particular package version; all other qualified goals must link. This is why the second path through the tree leads to failure, and the conflict set in this case contains the two qualified C goals (one of which must link to the other, although it doesn’t matter what links to what).
Backjumping
In this section we discuss in a bit more detail how backjumping works.
Accumulating conflict sets
In one previous example we had a package A-1.0 which depended on B-1.0 and a package A-2.0 which depended on B-2.0, but only B-1.0 was available; so, we could see we had a problem as soon as we picked a version for B.
Let’s modify the situation slightly so that we discover the problem a little later: A-1.0 depends on B-1.0, which in turn depends on C-1.0; similarly, A-2.0 depends on B-2.0 which in turn depends on C-2.0, but now only version 1.0 of C is available. Thus, after we pick a version for A, we will not detect the problem until we pick a version for C:
A-1.0 => B-1.0A-2.0 => B-2.0B-1.0 => C-1.0B-2.0 => C-2.0C-1.0
The search tree looks like this:
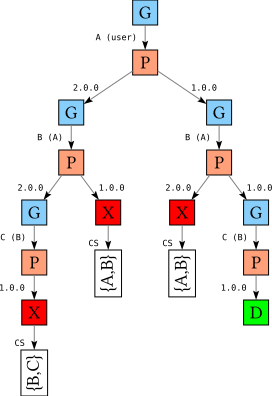
Let’s again concentrate on the left-most path through this tree:
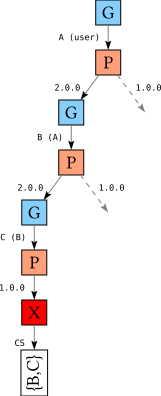
We pick version A-2.0, then B-2.0, and finally C-1.0; at this point we realize we have a problem: the version of C conflicts with the constraints on C imposed by B. Hence, the conflict set recorded on the failure node is the set {B,C}.
However, in order to resolve this failure, we actually need to pick a different version for A, which is not part of this conflict set! So how does that work? When we backtrack, and we encounter the P node for B; since B is part of the conflict set, we try a different version and follow the right path:
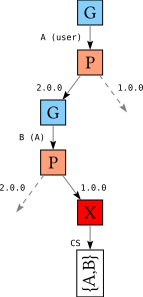
However, now we realize that this choice for B leads to a conflict between the choice for B and the constraints on B imposed by A: this path has a conflict set {A,B}. Then when we backtrack we union both conflict sets and continue backtracking with {A,B,C}, finally allowing us to make a different choice for A and finding the right solution.
Goal reasons
Fair warning: this is where things get a bit intricate.
Consider the following subtle variation on the above database; it is almost exactly the same, except that instead of having two versions B-1.0 and B-2.0, we instead have two different packages Ba-1.0 and Bb-1.0; the rest of the database is identical:
A-1.0 => Ba-1.0A-2.0 => Bb-1.0Ba-1.0 => C-1.0Bb-1.0 => C-2.0C-1.0
The search tree for this database looks as follows:
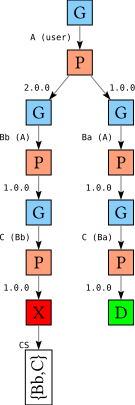
As before, if we follow the left-most path through this tree, we end up in a failure node with a conflict set {B,C}; notably, this conflict set does not contain A. However, unlike in the previous tree, when we start backtracking from this failure node, we don’t get an opportunity to make any different choice for B (Bb) and we never discover that we should A to the conflict set that we are accumulating. This would mean that when we see the choice for A, we don’t reconsider it and the solver would conclude that there is no solution.
So what is going on? One way to think about this is that actually we do have another option for the version of Bb: we can choose not to install Bb at all. After all, the only reason we are even considering Bb as a goal is because it was a dependency of A-2.0. If we make these choices explicit in the tree, it would look something like
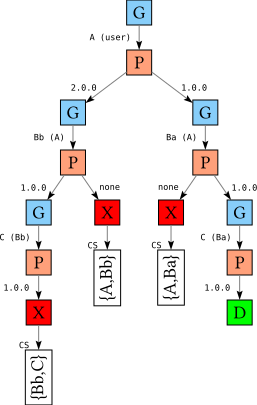
|

|
Search tree for Ba-1.0, Bb-1.0
|
Search tree for B-1.0, B-2.0(for comparison) |
|---|
On the left branch, choosing not to install Bb conflicts with the choice for A, since A-2.0 depends on Bb. If we express it like this, it becomes clear that when we explore this alternative choice for Bb we should add A into the conflict set we are accumulating.
The solver does not represent these “none” choices explicitly in the tree, however. Instead, whenever it is backjumping, it conservatively also adds the goal reason (the reason a goal was introduced) into the accumulated conflict set for every node it encounters as it backtracks. These goal reasons are the packages shown in parentheses in the search trees. (TODO: Isn’t this overly conservative? The tree with the explicit “none” choices suggests that it should suffice to add the goal reason for some goal into the accumulated conflict set only if that goal is part of the conflict set as well?)
NOTE: In the above discussion the goal reason is just another package; in the actual solver, we additionally record the package version. This is not used for backjumping but it helps in generating error messages: package Bb was introduced because we picked version 2.0 of A.
Non-determinism
In the search tree we only record a single goal reason for each goal; moreover, if one choice results in multiple conflicts, we only record one of them. In this somewhat more theoretical section we discuss why this is sound.
Goal reasons
Consider the database
A-1.0 => B-*, C-*B-1.0 => C-*C-1.0
The search tree for solving for A using this database looks like
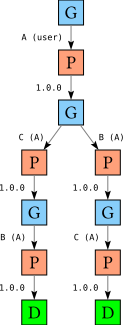
Note that the goal reason for C is recorded as A, not {A,B}. In this section we try to motivate why recording only one of the multiple goal reasons is sound.
Suppose we have a hypothetical tree that looks something like this:
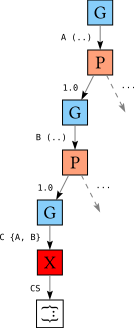
The tree is “hypothetical” in the sense that the goal reason for C is recorded as {A,B}; apparently, both A and B depend on C (as we saw, in reality only one of A and B will be recorded as the goal reason for C). Remember that the purpose of the goal reason is: if we cannot find any version of C that does not lead to a conflict, perhaps we can avoid the need for C at all by looking at why C was introduced into the tree. In this case, C was introduced because both A and B depend on it. Clearly, if we wanted to avoid C, we will have to make a different choice for both A and B.
The most efficient solution therefore is to pick A as the goal reason, and indeed this is the goal reason that the solver records. The question is whether it would also be correct to record B. Let’s consider the various possibilities carefully:
Perhaps there is a different choice of
Bthat does not depend onC. In this case, we will discover the other goal reason forCon that path.If all versions of
Bdepend onC, then in order to avoid introducingCinto the search tree we will need to avoid introducingBinto the search tree: we need to add the goal reason forBin the conflict set.- If this goal reason is
A, we’re good. - If this goal reason is a node above
A, then apparently we made a previous choice which depended onB, which in turn depends onC. Hence, picking a different version ofAwill not be sufficient and we can skip the choice forA. - If this goal reason is a node below
A, then we end up in a similar situation as we are in now, except now with two nodesA, B'whereB'is belowAbut aboveB, and we can proceed by induction.
- If this goal reason is
Conflict sets
Just like we can multiple goal reasons, we can also have multiple conflicts at a single node. For example, consider
A-1.0 => B-*, C-1.0B-1.0 => C-1.0C-1.0C-2.0
Solving for A:
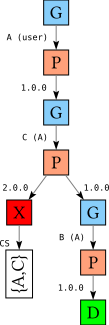
When we choose version 2.0 of C, we discover two conflicts: one between A and C, and one between B and C. However, only one of the two conflicts gets recorded; in this case, between A and C.
Abstracting, suppose package A and B both impose some bounds on package C that cannot be satisfied. We can draw an almost identical hypothetical tree as in the previous section:
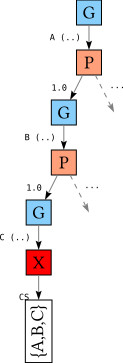
In this case the tree is hypothetical because the conflict set on C is recorded as {A,B,C} (again, as we saw, in reality only the conflict {A,C} or the conflict {B,C} will be recorded). As before, clearly we will need to make a different choice for both A and B to avoid this particular conflict. Thus picking {A,C} as the conflict set is the more efficient choice, and indeed this is what the solver does. (TODO: This happens in merge, and there is a comment there “I tried reverse here but it seemed to slow things down” – I’m pretty sure that that is because if you did call reverse, it effectively picks nodes lower down the tree rather than higher up the tree. But of course this kind of depends on exactly we call merge in various places. It would be nice if we could somehow make that more explicit.)
The question is, would the conflict set {B,C} also be correct? Let’s again consider what would happen:
- Suppose there is a version of
Bthat does not result in a conflict withC. In that case, we will recover the conflict set{A,C}on that path. - If there is no such choice, then we need to add the goal reason of
Binto the conflict set. This goal reason could beA, aboveA, or belowA; we proceed with a similar argument as in the previous section.
NOTE: In this example we illustrated that if we have two conflicts at a single node (one between A and C and another between B and C), it suffices to record only one. However, it is still important that for a single conflict we record all packages involved in that conflict, as discussed previously.
Conclusions
When the solver is traversing the tree looking for a solution and encounters a failure node, the conflict set recorded on that failure node records which choices the solver might reconsider in order to find a solution.
- If this conflict set is empty, it means that we have reached an actual failure and no matter what other choices we make, we will not be able to resolve this failure. When the solver encounters such a failure node it has no choice but to give up.
- On the other extreme, if the conflict set contains every single choice the solver has made leading up to the failure node, the solver will try to reconsider every choice it has made. This gives it the most leeway for finding a solution, but might mean it will unnecessarily reconsider choices that have no effect on the actual reason for the failure.
- Ideally, the conflict set contains only the choices that had some bearing on this particular failure. Constructing the smallest such conflict set however is not always an easy task, and occasionally we will over-approximate.
- If we detect a conflict, all choices involved in the conflict must be recorded in the conflict set, but if we detect multiple conflicts on the same node, we can pick just one of them; picking one that allows us to backjump further is more efficient.
